(本小题10分)“雪花曲线”因其形状类似雪花而得名,它可以以下列方式产生,如图,有一列曲线 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形,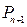 是对
是对 进行如下操作得到:将
进行如下操作得到:将 的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(
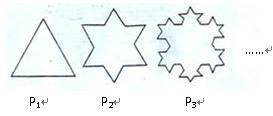
的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉( ).
).
(1)记曲线 的边长和边数分别为
的边长和边数分别为 和
和 (
(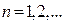 ),求
),求 和
和 的表达式;
的表达式;
(2)记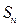 为曲线
为曲线 所围成图形的面积,写出
所围成图形的面积,写出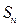 与
与 的递推关系式,并求
的递推关系式,并求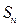 .
.
推荐套卷
(本小题10分)“雪花曲线”因其形状类似雪花而得名,它可以以下列方式产生,如图,有一列曲线 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形,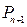 是对
是对 进行如下操作得到:将
进行如下操作得到:将 的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(
的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉( ).
).
(1)记曲线 的边长和边数分别为
的边长和边数分别为 和
和 (
(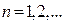 ),求
),求 和
和 的表达式;
的表达式;
(2)记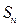 为曲线
为曲线 所围成图形的面积,写出
所围成图形的面积,写出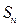 与
与 的递推关系式,并求
的递推关系式,并求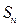 .
.