高中数学随机思想的发展试题

已知随机变量～，若,则

A．0

B．1

C．2

D．4

（本题12分）某种家电器每台的销售利润与该电器无故障使用时间T（单位：年）有关，若T≤1，则销售利润为0元，若1＜T≤3，则销售利润为100元，若T＞3，则销售利润为200元，设每台该种电台无故障使用时间T≤1，1＜T≤3及T＞3这三种情况发生的概率为为P₁，P₂，P₃，又知P₁，P₂是方程25x²－15x＋a＝0的两个根，且P₂＝P₃，
（1）求P₁，P₂，P₃的值；
（2）记表示销售两台这种家用电器的销售利润总和，求的分布列；
（3）求销售两台这种家用电器的销售利润总和的平均值。

（本小题满分12分）
某班级甲组有名学生，其中有名女生；乙组有名学生，其中有名女生.
（Ⅰ）若从两组中各抽取两人进行心理健康测试，求每组至少抽到一名女生的概率；
（Ⅱ）现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两组中共抽
取名学生进行心理健康测试.
（）求从甲、乙两组各抽取的人数；
（）记表示抽取的名学生中男生人数，求的分布列及数学期望.

某人5 次上班所花的时间（单位：分钟）分别为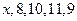，若这组数据的平均数为10，则其方差为     ▲   .

（本小题10分）口袋中有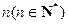个白球，3个红球．依次从口袋中任取一球，如果取到红球，那么继续取球，且取出的红球不放回；如果取到白球，就停止取球．记取球的次数为X．若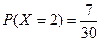，求：
（1）n的值；
（2）X的概率分布与数学期望．

(本小题满分12分)
某单位举办2010年上海世博会知识宣传活动，进行现场抽奖．盒中装有9张大小相同的精美卡片，卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案；抽奖规则是：参加者从盒中抽取卡片两张，若抽到两张都是“海宝”卡即可获奖，否则，均为不获奖．卡片用后放回盒子，下一位参加者继续重复进行．
(Ⅰ)活动开始后，一位参加者问：盒中有几张“海宝”卡?主持人答：我只知道，从盒中抽取两张都是“世博会会徽”卡的概率是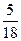，求抽奖者获奖的概率；
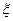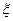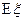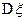(Ⅱ)现有甲乙丙丁四人依次抽奖，用表示获奖的人数，求的分布列及，的值．

为了更好地服务于2010年世博会，上海某酒店随机地对最近入住的名旅客进行服务质量问卷调查，把旅客对住宿的舒适满意度与价格满意度分为五个等级：
“1级（很不满意）”、“2级（不满意）”、“3级（一般）”、“4级（满意）”、“5级（很满意）”其结果如表所示，若在这个样本中，任选一人，其舒适度为，价格满意度.

(1)根据样本中的数据求P（y=5）及P（x≥3且y=3）的值；
(2)若的期望值为，求a、b、c的值；
(3)求该人在对价格满意（满意度不低于3）的条件下对舒适度也满意的概率.

上海世博会上有一种舞台灯，外形是正六棱柱，在其每个侧面（编号分别是①②③④⑤⑥）上安装5只颜色各异的灯，每只灯正常发光的概率是0.5，若一侧面上至少有3只灯发光，则不需要更换这个面，否则需要更换这个面，假定更换一个面需要100元，用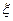表示更换费用。
（1）求①号面需要更换的概率；
（2）求6个侧面面上恰有2个侧面需要更换的概率。
（3）写出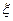的分布列，并求出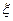的数学期望。

17．（本小题满分12分）
上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》，因其诞生于大芬村，因此被命名为《大芬丽莎》．某部门从参加创作的507名画师中随机抽出100名画师，测得画师年龄情况如下表所示．
（1）频率分布表中的①、②位置应填什么数据？并在答题卡中补全频率分布直方图（图4），再根据频率分布直方图估计这507个画师中年龄在岁的人数（结果取整数）；
（2）在抽出的100名画师中按年龄再采用分层抽样法抽取20人参加上海世博会深圳馆志愿者活动，其中选取2名画师担任解说员工作，记这2名画师中“年龄低于30岁”的人数为ξ，求ξ的分布列及数学期望．

分组 （单位：岁）	频数	频率
	5	0.050
	①	0.200
	35	②
	30	0.300
	10	0.100
合计	100	1.00

 

（本小题满分14分）
在一个盒子中，放有标号分别为1，2，3的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为x、y，设O为坐标原点，点P的坐标为记.
（1）求随机变量 的最大值，并求事件“取得最大值”的概率；
（2）求随机变量的分布列和数学期望.

从集合的所有非空子集中，等可能地取出一个.
（理）记所取出的非空子集中元素的个数为，则的数学期望=       .
（文）取出的非空子集中所有元素之和恰为6的概率=       .

一组数据为，，10，11，9，这组数据平均数为10，则方差的最小值为        .

（本小题满分12分）
甲、乙、丙三台机床各自独立的加工同一种零件，已知甲、乙、丙三台机床加工的零件是一等品的概率分别为0.7、0.6、0.8，乙、丙两台机床加工的零件数相等，甲机床加工的零件数是乙机床加工的零件的二倍。
（1）从甲、乙、丙加工的零件中各取一件检验，示至少有一件一等品的概率；
（2）将三台机床加工的零件混合到一起，从中任意的抽取一件检验，求它是一等品的概率；
（3）将三台机床加工的零件混合到一起，从中任意的抽取4件检验，其中一等品的个数记为X，求EX。

一只不透明的布袋中装有编号为1、2、3、4、5的五个大小形状完全一样的小球，现从袋中同时摸出只小球，用随机变量表示摸出的只球中的最大号码数，则随机变量的数学期望             ．

一组数据的平均数是，方差是 ，若将这组数据中的每一个数据都加上60，得到一组新数据，则所得新数据的平均数和方差分别是（   ）  

A．

B．

C．

D．