( 本小题满分12分) 某高校在上学期依次举行了“法律、环保、交通”三次知识竞赛活动,要求每位同学至少参加一次活动.该高校2014级某班50名学生在上学期参加该项活动的次数统计如图所示
(1)从该班中任意选两名学生,求他们参加活动次数不相等的概率.
(2)从该班中任意选两名学生,用 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
(3)从该班中任意选两名学生,用 表示这两人参加活动次数之和,记“函数
表示这两人参加活动次数之和,记“函数 在区间(3,5)上有且只有一个零点”为事件A,求事件A发生的概率.
在区间(3,5)上有且只有一个零点”为事件A,求事件A发生的概率.
相关知识点
推荐套卷
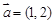 ,
,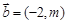 ,
, ,
, ,
,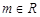 ,
, 为正实数.
为正实数.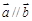 ,求
,求 的值;
的值; ,求
,求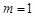 时,若
时,若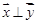 ,试确定
,试确定 与
与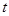 的关系式.
的关系式. 其中
其中 .(1)求函数
.(1)求函数 的单调区间;(2)若函数
的单调区间;(2)若函数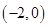 内恰有两个零点,求
内恰有两个零点,求 的取值范围;
的取值范围;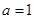 时,设函数
时,设函数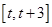 上的最大值为
上的最大值为 最小值为
最小值为 ,记
,记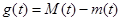 ,求函数
,求函数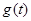 在区间
在区间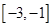 上的最小值.
上的最小值.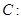
 (
( )的一个顶点为
)的一个顶点为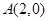 ,离心率为
,离心率为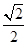 ,直线
,直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 、
、 .(1) 求椭圆
.(1) 求椭圆 的面积为
的面积为 时,求
时,求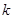 的值.
的值.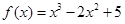 在区间
在区间 上的最值.
上的最值.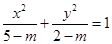 (
(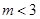 )所表示的曲线类型.
)所表示的曲线类型. 粤公网安备 44130202000953号
粤公网安备 44130202000953号