设P(a,b)(b≠0)是平面直角坐标系xOy中的点,l是经过原点与点(1,b)的直线,记Q是直线l与抛物线x2=2py(p≠0)的异于原点的交点
⑴.已知a=1,b=2,p=2,求点Q的坐标。
⑵.已知点P(a,b)(ab≠0)在椭圆+y2=1上,p=,求证:点Q落在双曲线4x2-4y2=1上。
⑶.已知动点P(a,b)满足ab≠0,p=,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由。
已知抛物线y=x2-1上一定点B(-1,0)和两个动点P、Q,当P在抛物线上运动时,BP⊥PQ,则Q点的横坐标的取值范围是_________
直线l的方程为y=x+3,在l上任取一点P,若过点P且以双曲线12x2-4y2=3的焦点作椭圆的焦点,那么具有最短长轴的椭圆方程为_________
点A、B分别是椭圆 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于 轴上方,
轴上方, .
.
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离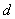 的最小值.
的最小值.
抛物线C的方程为 ,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足
,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足 .
.
(Ⅰ)求抛物线C的焦点坐标和准线方程;
(Ⅱ)设直线AB上一点M,满足 ,证明线段PM的中点在y轴上;
,证明线段PM的中点在y轴上;
(Ⅲ)当 =1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标
=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标 的取值范围.
的取值范围.
如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得 试建立适当的坐标系,并求动点 P的轨迹方程.
试建立适当的坐标系,并求动点 P的轨迹方程.

抛物线的顶点在原点,焦点在y轴上,抛物线上一点P(m,-3)到焦点的距离为5,则抛物线的准线方程是( )
| A.y=4 | B.y=-4 | C.y=2 | D.y=-2 |