设P(a,b)(b≠0)是平面直角坐标系xOy中的点,l是经过原点与点(1,b)的直线,记Q是直线l与抛物线x2=2py(p≠0)的异于原点的交点
⑴.已知a=1,b=2,p=2,求点Q的坐标。
⑵.已知点P(a,b)(ab≠0)在椭圆+y2=1上,p=,求证:点Q落在双曲线4x2-4y2=1上。
⑶.已知动点P(a,b)满足ab≠0,p=,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由。
相关知识点
推荐套卷
 的前
的前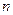 项和为
项和为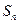 ,且
,且 ,
, .
.  ;
;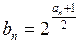 ,求数列
,求数列 的前n项和
的前n项和 .
.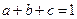 ,且
,且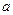 .
.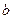 .
.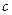 是正数,求证:
是正数,求证: .
.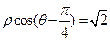 ,曲线C的参数方程为
,曲线C的参数方程为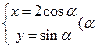 为参数),求曲线C截直线l所得的弦长
为参数),求曲线C截直线l所得的弦长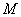 是把坐标平面上的点的横坐标伸长到
是把坐标平面上的点的横坐标伸长到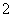 倍,纵坐标伸长到
倍,纵坐标伸长到 倍的伸压变换.
倍的伸压变换. 以及椭圆
以及椭圆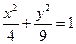 在
在
 成立,求实数a的取值范围;
成立,求实数a的取值范围; 在[0,2]上恰有两个不同的实根,求实数b的取值范围.
在[0,2]上恰有两个不同的实根,求实数b的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号