我县某中学为了配备高一新生中寄宿生的用品，招生前随机抽取部分准高一学生调查其上学路上所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中上学路上所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．
（1）求直方图中
的值；
（2）如果上学路上所需时间不少于40分钟的学生应寄宿，且该校计划招生1800名，请估计新生中
应有多少名学生寄宿；
（3）若不安排寄宿的话，请估计所有学生上学的平均耗时（用组中值代替各组数据的平均值）．
（本小题满分12分）某城市100户居民的月平均用电量（单位：度），以[160，180），[180，200），[200，200），[220．240），[240，260），[260，280），[280，300）分组的频率分布直方图如图．
（1）求月平均用电量的众数和中位数；
（2）在月平均用电量为[220．240），[240，260），[260，280），[280，300）的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[240．260）的用户中应抽取多少户？
某城市100户居民的月平均用电量（单位：度），以[160，180），[180，200），[200，200），[220．240），[240，260），[260，280），[280，300）分组的频率分布直方图如图．
（1）求直方图中x的值；
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量为，[220，240），[240，260），[260，280），[280，300）的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[220，240）的用户中应抽取多少户？
从两块玉米地里各抽取10株玉米苗，分别测得它们的株高如下（单位：cm ）：
甲：25 41 40 37 22 14 19 39 21 42 乙：27 16 44 27 44 16 40 40 16 40
根据以上数据回答下面的问题：
（1）哪种玉米苗长得高？
（2）哪种玉米苗长得齐？
（本小题满分10分）某地区100位居民的人均月用水量（单位：t）的频率分布直方图及频数分布表如下：
| 分组 |
频数 |
| [0，0．5） |
4 |
| [0．5，1） |
8 |
| [1，1．5） |
15 |
| [1．5，2） |
22 |
| [2，2．5） |
25 |
| [2．5，3） |
14 |
| [3，3．5） |
6 |
| [3．5，4） |
4 |
| [4，4．5] |
2 |
| 合计 |
100 |
（1）根据频率分布直方图估计这组数据的众数与平均数；
（2）当地政府制定了人均月用水量为3t的标准，若超出标准加倍收费，当地政府解释说，85%以上的居民不超出这个标准，这个解释对吗？为什么？
在每年的春节后，某市政府都会发动公务员参与到植树绿化活动中去．林业管理部门在植树前，为了保证树苗的质量，都会在植树前对树苗进行检测．现从甲、乙两种树苗中各抽测了10株树苗，量出它们的高度如下（单位：厘米）：
甲：37，21，31，20，29，19，32，23，25，33；
乙：10，30，47，27，46，14，26，10，44，46．
（1）画出两组数据的茎叶图，并根据茎叶图对甲、乙两种树苗的高度作比较，写出两个统计结论；
（2）设抽测的10株甲种树苗高度平均值为
，将这10株树苗的高度依次输入，按程序框（如图）进行运算，问输出的S大小为多少？并说明S的统计学意义．
（本小题满分14分）下面的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩（单位:分）．已知甲代表队数据的中位数为76，乙代表队数据的平均数是75．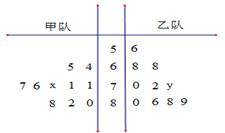
（1）求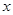
，
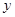的值；
（2）若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生，求抽到的学生中，甲队学生成绩不低于乙队学生成绩的概率；
（3）判断甲、乙两队谁的成绩更稳定，并说明理由（方差较小者稳定）．
为了解一大片经济林生长情况，随机测量其中的60株的底部周长（单位：Cm），将周长整理后画出的频率分布表和频率分布直方图如下：观察图形，回答下列问题：
| 组距 |
频数 |
频率 |
|
 [ |
6 |
0．1 |
|
 |
|
0．15 |
|
 |
9 |
|
|
 |
18 |
|
|
 |
|
0．25 |
|
 |
3 |
0．05 |
|
| 合计 |
|
|
（1）补充上面的频率分布表和频率分布直方图．
（2）79．5~89．5 这一组的频数、频率分别是多少？
（3）估计这次环保知识竞赛的及格率（60cm及以上为合格
（本小题12分）根据国家环保部新修订的《环境空气质量标准》规定：居民区PM2．5的年平均浓度不得超过35微克/立方米，PM2．5的24小时平均浓度不得超过75微克/立方米．某城市环保部门随机抽取了一居民区去年20天PM2．5的24小时平均浓度的监测数据，数据统计如下：
]
| 组别 |
PM2.5浓度（微克/立方米） |
频数（天） |
频率 |
| 第一组 |
 |
3 |
0.15 |
| 第二组 |
 |
12 |
0.6 |
| 第三组 |
 |
3 |
0.15 |
| 第四组 |
 |
2 |
0.1 |
（Ⅰ）从样本中PM2．5的24小时平均浓度超过50微克/立方米的5天中，随机抽取2天，求恰好有一天PM2．5的24小时平均浓度超过75微克/立方米的概率；
（Ⅱ）求样本平均数，并根据样本估计总体的思想，从PM2．5的年平均浓度考虑，判断该居民区的环境是否需要改进？说明理由．
从高三抽出50名学生参加数学竞赛，由成绩得到如下的频率分布直方图．由于一些数据丢失，试利用频率分布直方图求：
（1）这50名学生成绩的众数与中位数．
（2）这50名学生的平均成绩．
某工厂对某产品的产量与单位成本的资料分析后有如下数据：
| 月 份 |
1 |
2 |
3 |
4 |
5 |
6 |
| 产量x千件 |
2 |
3 |
4 |
3 |
4 |
5 |
| 单位成本y元/件 |
73 |
72 |
71 |
73 |
69 |
68 |
（Ⅰ）求单位成本y与月产量x之间的线性回归方程．（其中已计算得：
，结果保留两位小数）
（Ⅱ）当月产量为12千件时,单位成本是多少?
（本小题满分12分）在2015年全运会上两名射击运动员甲、乙在比赛中打出如下成绩：
甲：9．4，8．7，7．5，8．4，10．1，10．5，10．7，7．2，7．8，10．8；
乙：9．1，8．7，7．1，9．8，9．7，8．5，10．1，9．2，10．1，9．1；
（1）用茎叶图表示甲、乙两人的成绩；并根据茎叶图估计他们的中位数；
（2）已知甲、乙两人成绩的方差分别为
与
，分别计算两个样本的平均数
和标准差
，并根据计算结果估计哪位运动员的成绩比较好，哪位运动员的成绩比较稳定．
对甲、乙两名自行车赛手在相同条件下进行了6次测试，测得他们的最大速度（m/s）的数据如下表．
| 次数 |
1 |
2 |
3 |
4 |
5 |
6 |
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |
（1）画出茎叶图，由茎叶图判断哪位选手的成绩较稳定？
（2）分别求出甲、乙两名自行车赛手最大速度（m/s）数据的平均数、中位数、标准差，并判断选谁参加
比赛更合适．
以下茎叶图记录了甲、乙两名射击运动员训练的成绩（环数），射击次数为4次．
（1）试比较甲、乙两名运动员射击水平的稳定性；
（2）每次都从甲、乙两组数据中随机各选取一个进行比对分析，共选取了4次（有放回选取）．设选取的两个数据中甲的数据大于乙的数据的次数为
，求的分布列及数学期望．
粤公网安备 44130202000953号
