以下茎叶图记录了甲、乙两名射击运动员训练的成绩（环数），射击次数为4次．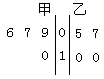
（1）试比较甲、乙两名运动员射击水平的稳定性；
（2）每次都从甲、乙两组数据中随机各选取一个进行比对分析，共选取了4次（有放回选取）．设选取的两个数据中甲的数据大于乙的数据的次数为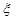
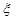，求的分布列及数学期望．
，则
在R上是增函数；
，则
ABC是
；
的最小值为
；
，则A=B；
，则
，
、
，求
的值？
时，不等式：
恒成立，求实数
的范围．
，求
的最大值；
相关知识点
推荐套卷
以下茎叶图记录了甲、乙两名射击运动员训练的成绩（环数），射击次数为4次．
（1）试比较甲、乙两名运动员射击水平的稳定性；
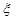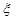（2）每次都从甲、乙两组数据中随机各选取一个进行比对分析，共选取了4次（有放回选取）．设选取的两个数据中甲的数据大于乙的数据的次数为，求的分布列及数学期望．
粤公网安备 44130202000953号