(本小题满分12分)如下图所示,从参加环保知识竞赛的学生中抽出60名,将其成绩整理后画出的频率分布直方图,观察图形,回答下列问题:
(Ⅰ) 这一组的频率和频数分别为多少?
这一组的频率和频数分别为多少?
(Ⅱ)估计这次环保知识竞赛的平均成绩。
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是: ,
, ,
, ,
, ,
, .
.
(Ⅰ)求图中 的值;
的值;
(Ⅱ)根据直方图,估计这100名学生语文成绩的平均分;
(Ⅲ)若这100名学生语文成绩某些分数段的人数 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数 之比如下表所示,求数学成绩在
之比如下表所示,求数学成绩在 之外的人数.
之外的人数.
| 分数段 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(本小题满分12分)贵阳市某中学高三第一次摸底考试中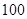 名学生数学成绩的频率分布直方图如图
名学生数学成绩的频率分布直方图如图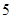 所示,其中成绩分组区间是
所示,其中成绩分组区间是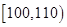 ,
,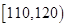 ,
,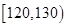 ,
, ,
,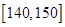 .
.
(Ⅰ)求图中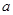 的值;
的值;
(Ⅱ)根据频率分布直方图,估计这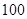 名学生数学成绩的平均分;
名学生数学成绩的平均分;
(Ⅲ)若这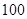 名学生数学成绩某些分数段的人数(
名学生数学成绩某些分数段的人数( )与语文成绩相应分数段的人数(
)与语文成绩相应分数段的人数(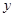 )之比如下表所示,求语文成绩在
)之比如下表所示,求语文成绩在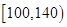 之外的人数.
之外的人数.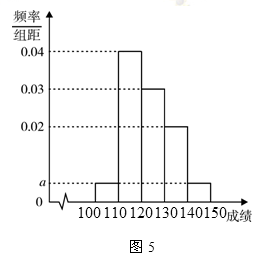

为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前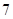 次考试的数学成绩
次考试的数学成绩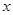 、物理成绩
、物理成绩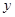 进行分析.下面是该生
进行分析.下面是该生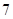 次考试的成绩.
次考试的成绩.
| 数学 |
88 |
83 |
117 |
92 |
108 |
100 |
112 |
| 物理 |
94 |
91 |
108 |
96 |
104 |
101 |
106 |
(1)他的数学成绩与物理成绩哪个更稳定?请给出你的理由;
(2)已知该生的物理成绩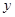 与数学成绩
与数学成绩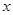 是线性相关的,若该生的物理成绩达到
是线性相关的,若该生的物理成绩达到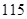 分,请你估计他的数学成绩大约是多少?
分,请你估计他的数学成绩大约是多少?
(已知88 94+83
94+83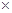 91+117
91+117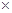 108+92
108+92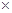 96+108
96+108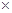 104+100
104+100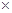 101+112
101+112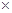 106=70497,
106=70497,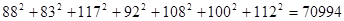 )
)
(参考公式: ,
,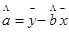 )
)
(本小题满分12分)某中学随机抽取部分高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
, ,
, .
.
(1)求直方图中 的值;
的值;
(2)如果上学路上所需时间不少于小时的学生可申请在学校住宿,若招生 名,请估计新生中有多少名学生可以申请住宿;
名,请估计新生中有多少名学生可以申请住宿;
(3)从学校的高一学生中任选4名学生,这4名学生中上学路上所需时间少于20分钟的人数记为 ,求
,求 的分布列和数学期望.(以直方图中的频率作为概率).
的分布列和数学期望.(以直方图中的频率作为概率).
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
| 质量指标值分组 |
[75,85) |
[85,95) |
[95,105) |
[105,115) |
[115,125) |
| 频数 |
6 |
26 |
38 |
22 |
8 |
(1)在答题卡上作出这些数据的频率分布直方图 (用阴影表示)
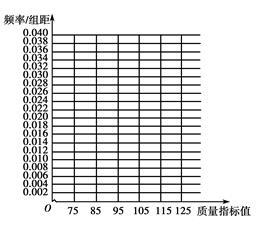
(2)估计这种产品质量指标值的平均数及中位数
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
(本小题满分12分)某校为了响应《中共中央国务院关于加强青少年体育增强青少年体质的意见》精神,落实“生命—和谐”教育理念和阳光体育行动的现代健康理念,学校特组织“踢毽球”大赛,某班为了选出一人参加比赛,对班上甲乙两位同学进行了 次测试,且每次测试之间是相互独立.成绩如下:(单位:个/分钟)
次测试,且每次测试之间是相互独立.成绩如下:(单位:个/分钟)
| 甲 |
80 |
81 |
93 |
72 |
88 |
75 |
83 |
84 |
| 乙 |
82 |
93 |
70 |
84 |
77 |
87 |
78 |
85 |
(1)用茎叶图表示这两组数据
(2)从统计学的角度考虑,你认为选派那位学生参加比赛合适,请说明理由?
(3)若将频率视为概率,对甲同学在今后的三次比赛成绩进行预测,记这三次成绩高于 个/分钟的次数为
个/分钟的次数为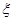 ,求
,求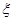 的分布列及数学期望
的分布列及数学期望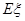 .
.
(参考数据: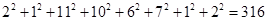 ,
,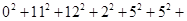
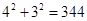 )
)
为了了解小学五年级学生的体能情况,抽取了实验小学五年级部分学生进行踢毽子测试,将所得的数据整理后画出频率分布直方图(如图),已知图中从左到右的前三个小组的频率分别是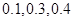 ,第一小组的频数是
,第一小组的频数是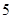 .
.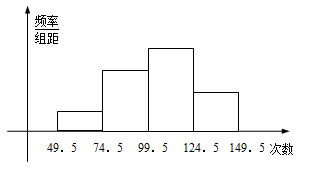
(Ⅰ)求第四小组的频率和参加这次测试的学生人数;
(Ⅱ)在这次测试中,问学生踢毽子次数的中位数落在第几小组内?
(Ⅲ)在这次跳绳测试中,规定跳绳次数在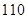 以上的为优秀,试估计该校此年级跳绳成绩的优秀率是多
以上的为优秀,试估计该校此年级跳绳成绩的优秀率是多
少?
为了调查某校学生体质健康达标情况,现采用随机抽样的方法从该校抽取了m名学生进行体育测试. 根据体育测试得到了这m名学生各项平均成绩(满分100分),按照以下区间分为七组: ,
, ,并得到频率分布直方图(如图),已知测试平均成绩在区间
,并得到频率分布直方图(如图),已知测试平均成绩在区间 有20人.
有20人.
(1)求m的值及中位数n;
(2)若该校学生测试平均成绩小于n,则学校应适当增加体育活动时间,根据以上抽样调查数据,该校是否需要增加体育活动时间?
(本小题满分12分)在2015年全运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲、乙两人的成绩;并根据茎叶图估计他们的中位数;
(2)已知甲、乙两人成绩的方差分别为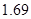 与
与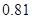 ,分别计算两个样本的平均数
,分别计算两个样本的平均数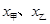 和标准差
和标准差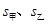 ,并根据计算结果估计哪位运动员的成绩比较好,哪位运动员的成绩比较稳定.
,并根据计算结果估计哪位运动员的成绩比较好,哪位运动员的成绩比较稳定.
某地区为了了解某地区高中生的身体发育情况,对某一中学的随机抽取的50名学生的体重进行了测量,结果如下:(单位:kg)
42,38,29,36,41,43,54,43,34,44,40,59,39,42,44,50,37,44,45,29,48,45,53,48,37,28,46,50,37,44,
42,39,51,52,62,47,59,46,45,,67,53,49,65,47,54,63,58,43,46,58.
| 分组 |
频数 |
频率 |
频率/组距 |
| [27,32) |
|
0.06 |
|
| [32,37) |
|
0.06 |
|
| [37,42) |
9 |
|
|
| [42,47) |
|
|
0.064 |
| [47,52) |
7 |
|
|
| [52,57) |
5 |
|
|
| [57,62) |
4 |
|
|
| [62,67) |
|
0.06 |
|
(1)若以组距为5,完成下面样本频率分布表:
(2)根据(1)中的频率分布表,画出频率分布直方图;
(3)若本地区学生总人数为3000人,试根据抽样比例,估计本地区学生体重在区间[37,57]内所占的人数约为多少人?
某中学将100名高一新生分成水平相同的甲,乙两个“平行班”,每班50人。陈老师采用A,B两种不同的教学方式分别在甲,乙两个班级进行教改实验。为了解教学效果,期末考试后,陈老师对甲,乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图),计成绩不低于90分者为“成绩优秀”.
从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
根据频率分布直方图填写下面2x2列联表,并判断是否有 的把握认为“成绩优秀”与教学方式有关.
的把握认为“成绩优秀”与教学方式有关.
| |
甲班(A方式) |
乙班(B方式) |
总计 |
| 成绩优秀 |
|
|
|
| 成绩不优秀 |
|
|
|
| 总计 |
|
|
|
附:
P( |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
| k |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
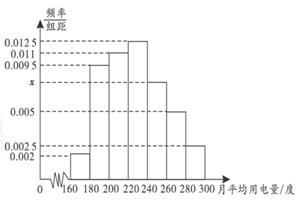
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,整理得到数据分组及频率分布表和频率分布直方图:
| 分组(日销售量) |
频率(甲种酸奶) |
| [0,10] |
0.10 |
| (10,20] |
0.20 |
| (20,30] |
0.30 |
| (30,40] |
0.25 |
| (40,50] |
0.15 |

(Ⅰ)写出频率分布直方图中的a的值,并作出甲种酸奶日销售量的频率分布直方图;
(Ⅱ)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为 ,试比较
,试比较 与
与 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计乙种酸奶在未来一个月(按30天计算)的销售总量.
(本小题满分12分)为了分析某次考试数学成绩情况,用简单随机抽样从某班中抽取25名学生的成绩(百分制)作为样本,得到频率分布表如下:
| 分数 |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
| 频数 |
2 |
3 |
9 |
a |
1 |
| 频率 |
0.08 |
0.12 |
0.36 |
b |
0.04 |
(Ⅰ)求样本频率分布表中a,b的值,并根据上述频率分布表,在下表中作出样本频率分布直方图;
(Ⅱ)计算这25名学生的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)从成绩在[50,70)的学生中任选2人,求至少有1人的成绩在[60,70)中的概率.