(本小题满分12分)在2015年全运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲、乙两人的成绩;并根据茎叶图估计他们的中位数;
(2)已知甲、乙两人成绩的方差分别为 与
与 ,分别计算两个样本的平均数
,分别计算两个样本的平均数 和标准差
和标准差 ,并根据计算结果估计哪位运动员的成绩比较好,哪位运动员的成绩比较稳定.
,并根据计算结果估计哪位运动员的成绩比较好,哪位运动员的成绩比较稳定.
相关知识点
推荐套卷
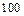 人的成绩作为样本.对高一年级的
人的成绩作为样本.对高一年级的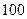 名学生的成绩进行统计,并按
名学生的成绩进行统计,并按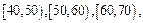
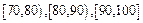 分组,得到成绩分布的频率分布直方图(如图).
分组,得到成绩分布的频率分布直方图(如图).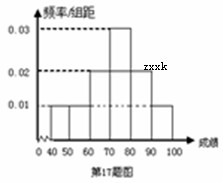
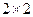 列联表,并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系”。
列联表,并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系”。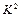 的公式
的公式 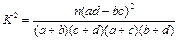
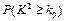
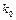
 的图象与直线
的图象与直线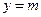 相切,相邻切点之间的距离为
相切,相邻切点之间的距离为 .
.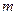 的值;
的值;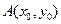 是
是 图象的对称中心,且
图象的对称中心,且 ,求点
,求点 的坐标.
的坐标. 在
在 处取得极值5,
处取得极值5,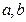 的值;
的值; 上的最大值
上的最大值 粤公网安备 44130202000953号
粤公网安备 44130202000953号