福建省四地六校高二上学期11月月考理科数学试卷
若命题p:∀x∈R,2x2+1>0,则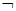 p是( )
p是( )
| A.∀x∈R,2x2+1≤0 | B.∃x∈R,2x2+1>0 |
| C.∃x∈R,2x2+1<0 | D.∃x∈R,2x2+1≤0 |
在△ABC中,“A>60°”是 “ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
统计某校1 000名学生的数学测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是( )

| A.20% | B.25% | C.60% | D.80% |
为了解某地区的中小学生视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已了解到该地区小学,初中,高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大,在下面的抽样方法中,最合理的抽样方法是( )
| A.简单随机抽样 | B.按性别分层抽样 |
| C.按学段分层抽样 | D.系统抽样 |
阅读下边的程序框图,运行相应的程序,输出S的值为( )

| A.15 | B.245 | C.105 | D.945 |
我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1530石,验得米内夹谷,抽样取米一把,数得253粒内夹谷28粒,则这批米内夹谷约为( )
| A.144石 | B.169石 | C.338石 | D.1365石 |
从1,2,3,4,5中任意选取3个不同的数,则取出的3个数能够作为三角形的三边边长的概率是( )
A. |
B. |
C. |
D. |
命题p:关于x的不等式(x-2)  ≥0的解集为{x|x≥2},命题q:若函数y=kx2-kx-1的值恒小于0,则-4<k≤0,那么不正确的是( )
≥0的解集为{x|x≥2},命题q:若函数y=kx2-kx-1的值恒小于0,则-4<k≤0,那么不正确的是( )
A.“ p”为假命题 p”为假命题 |
B.“  q”为假命题 q”为假命题 |
| C.“p且q”为真命题 | D.“p或q”为假命题 |
甲,乙两队进行排球决赛,现在的情形是甲队只要再赢一局就获冠军,乙队需要再赢两局才能得冠军,若两队胜每局的概率相同,则甲队获得冠军的概率为( )
A. |
B.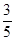 |
C.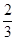 |
D.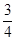 |
过双曲线 的右焦点
的右焦点 作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为A,B,若
作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为A,B,若 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A. |
B. |
C. |
D. |
如图,已知椭圆 的左,右焦点分别为
的左,右焦点分别为 ,
, ,
, 是
是 轴正半轴上一点,
轴正半轴上一点, 交椭圆于A,若
交椭圆于A,若 ,且
,且 的内切圆半径为
的内切圆半径为 ,则椭圆的离心率为( )
,则椭圆的离心率为( )

A. |
B. |
C. |
D. |
下表是某厂1~4月份用水量(单位:百吨)的一组数据:
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
由其散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是
 =-0.7x+
=-0.7x+ ,则
,则 = .
= .
如图,在矩形ABCD中,AB= ,BC=1,以A为圆心,1为半径作四分之一个圆弧DE,在圆弧DE上任取一点P,则直线AP与线段BC有公共点的概率是 .
,BC=1,以A为圆心,1为半径作四分之一个圆弧DE,在圆弧DE上任取一点P,则直线AP与线段BC有公共点的概率是 .

在 中,BC边长为24,AC、AB边上的中线长之和等于39.若以BC边中点为原点,BC
中,BC边长为24,AC、AB边上的中线长之和等于39.若以BC边中点为原点,BC
边所在直线为x轴建立直角坐标系,则 的重心G的轨迹方程为: .
的重心G的轨迹方程为: .
已知命题p:方程 表示焦点在
表示焦点在 轴上的双曲线,命题q:f(x)=-(5-2m)x是减函数,若p或q为真命题,p且q为假命题,求实数m的取值范围
轴上的双曲线,命题q:f(x)=-(5-2m)x是减函数,若p或q为真命题,p且q为假命题,求实数m的取值范围
以下茎叶图记录了甲,乙两组各四名同学的植树棵树,乙组记录中有一个数据模糊,无法确认,在图中以X表示。
(1)如果X=8,求乙组同学植树棵树的平均数和方差;
(2)如果X=9,分别从甲,乙两组中随机选取一名同学,求这两名同学的植树总棵树为19的概率.
已知椭圆C的两焦点分别为 ,长轴长为6,
,长轴长为6,
(1)求椭圆C的标准方程;
(2)已知过点(0,2)且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
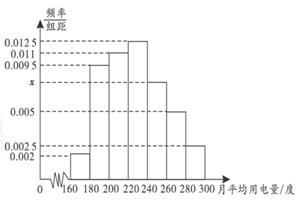
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
某地区2007年至2013年农村居民家庭纯收入 (单位:千元)的数据如下表
(单位:千元)的数据如下表
| 年份 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
年份代号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
人均纯收入 |
2.9 |
3.3 |
3.6 |
4.4 |
4.8 |
5.2 |
5.9 |
(1)求y关于 的线性回归方程
的线性回归方程
(2)判断y与 之间是正相关还是负相关?
之间是正相关还是负相关?
(3)预测该地区2015年农村居民家庭人均纯收入。
附:回归直线的斜率和截距的最小二乘法估计公式分别为: ,
,
 的一个焦点是
的一个焦点是 ,那么实数
,那么实数 的值为( )
的值为( ) 与
与 轴,
轴, 轴的正半轴分别交于A,B两点,原点O到直线AB的距离为
轴的正半轴分别交于A,B两点,原点O到直线AB的距离为 该椭圆的离心率为
该椭圆的离心率为
 的直线
的直线 与椭圆交于M,N两个不同的点,使
与椭圆交于M,N两个不同的点,使 成立?若存在,求出
成立?若存在,求出 粤公网安备 44130202000953号
粤公网安备 44130202000953号