（本小题满分12分）某校高三文科分为四个班．高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人．抽取出来的所有学生的测试成绩统计结果的频率分布条形图如下图所示,其中120～130（包括120分但不包括130分）的频率为0．05,此分数段的人数为5人．
（1）问各班被抽取的学生人数各为多少人?
（2）求平均成绩.
（3）在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率．
（本小题满分12分）对甲､乙的学习成绩进行抽样分析,各抽5门功课,得到的观测值如下
| 甲 |
60 |
80 |
70 |
90 |
70 |
| 乙 |
80 |
60 |
70 |
80 |
75 |
问:甲､乙两人谁的平均成绩高?谁的各门功课发展较平衡?
为了了解初三学生女生身高情况，某中学对初三女生身高进行了一次测量，所得数据整理后列出了频率分布表如下：
| 组 别 |
频数 |
频率 |
| 145．5～149．5 |
1 |
0．02 |
| 149．5～153．5 |
4 |
0．08 |
| 153．5～157．5 |
20 |
0．40 |
| 157．5～161．5 |
15 |
0．30 |
| 161．5～165．5 |
8 |
0．16 |
| 165．5～169．5 |
m |
n |
| 合 计 |
M |
N |
（1）求出表中
所表示的数分别是多少？
（2）画出频率分布直方图．
（3）全体女生中身高在哪组范围内的人数最多？
在每年的春节后，某市政府都会发动公务员参与到植树绿化活动中去．林业管理部门在植树前，为了保证树苗的质量，都会在植树前对树苗进行检测．现从甲、乙两种树苗中各抽测了10株树苗，量出它们的高度如下（单位：厘米）：
甲：37，21，31，20，29，19，32，23，25，33；
乙：10，30，47，27，46，14，26，10，44，46．
（1）画出两组数据的茎叶图，并根据茎叶图对甲、乙两种树苗的高度作比较，写出两个统计结论；
（2）设抽测的10株甲种树苗高度平均值为
，将这10株树苗的高度依次输入，按程序框（如图）进行运算，问输出的S大小为多少？并说明S的统计学意义．
某农场计划种植某种新作物，为此对这种作物的两个品种（分别称为品种甲和品种乙）进行田间试验．选取两大块地，每大块地分成
小块地，在总共
小块地中，随机选小块地种植品种甲，另外小块地种植品种乙．
（1）假设
，求第一大块地都种植品种甲的概率；
（2）试验时每大块地分成
小块，即
，试验结束后得到品种甲和品种乙在各小块地上的每公顷产量（单位：kg/hm2）如下表：
| 甲 |
 |
 |
 |
 |
 |
 |
 |
 |
| 乙 |
 |
|
|
 |
 |
 |
|
 |
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种?
（本小题满分12分）某城市
户居民的月平均用电量（单位：度），以
，
，
，
，
，
，
分组的频率分布直方图如图．
（1）求直方图中
的值；
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取
户居民，则月平均用电量在的用户中应抽取多少户？
假定下述数据是甲、乙两个供货商的交货天数：
甲：10 9 10 10 11 11 9 11 10 10
乙：8 10 14 7 10 11 10 8 15 12
估计两个供货商的交货情况，并问哪个供货商交货时间短一些，哪个供货商交货时间较具一致性与可靠性．
（本小题满分14分）下面的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩（单位:分）．已知甲代表队数据的中位数为76，乙代表队数据的平均数是75．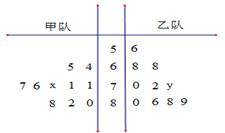
（1）求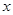
，
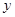的值；
（2）若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生，求抽到的学生中，甲队学生成绩不低于乙队学生成绩的概率；
（3）判断甲、乙两队谁的成绩更稳定，并说明理由（方差较小者稳定）．
某市交管部门为了宣传新交规举办交通知识问答活动，随机对该市15～65岁的人群抽样，回答问题统计结果如图表所示．
| 组别 |
分组 |
回答正确的人数 |
回答正确的人数占本组的概率 |
| 第1组 |
[15,25) |
5 |
0.5 |
| 第2组 |
[25,35) |
 |
0.9 |
| 第3组 |
[35,45) |
27 |
 |
| 第4组 |
[45,55) |
 |
0.36 |
| 第5组 |
[55,65) |
3 |
 |
（1）分别求出
的值；
（2）从第2，3，4组回答正确的人中用分层抽样方法抽取6人，则第2，3，4组每组应各抽取多少人?
（3）在（2）的前提下，决定在所抽取的6人中随机抽取2人颁发幸运奖，求：所抽取的人中第2组至少有1人获得幸运奖的概率．
甲、乙两同学的6次考试成绩分别为:
| 甲 |
 |
 |
 |
 |
 |
|
| 乙 |
|
 |
 |
|
 |
|
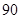（Ⅰ）画出甲、乙两同学6次考试成绩的茎叶图；
（Ⅱ）计算甲、乙两同学考试成绩的方差，并对甲、乙两同学的考试成绩做出合理评价．
某工厂对某产品的产量与单位成本的资料分析后有如下数据：
| 月 份 |
1 |
2 |
3 |
4 |
5 |
6 |
| 产量x千件 |
2 |
3 |
4 |
3 |
4 |
5 |
| 单位成本y元/件 |
73 |
72 |
71 |
73 |
69 |
68 |
（Ⅰ）求单位成本y与月产量x之间的线性回归方程．（其中已计算得：
，结果保留两位小数）
（Ⅱ）当月产量为12千件时,单位成本是多少?
对甲、乙两名自行车赛手在相同条件下进行了6次测试，测得他们的最大速度（m/s）的数据如下表．
| 次数 |
1 |
2 |
3 |
4 |
5 |
6 |
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |
（1）画出茎叶图，由茎叶图判断哪位选手的成绩较稳定？
（2）分别求出甲、乙两名自行车赛手最大速度（m/s）数据的平均数、中位数、标准差，并判断选谁参加
比赛更合适．
以下茎叶图记录了甲、乙两名射击运动员训练的成绩（环数），射击次数为4次．
（1）试比较甲、乙两名运动员射击水平的稳定性；
（2）每次都从甲、乙两组数据中随机各选取一个进行比对分析，共选取了4次（有放回选取）．设选取的两个数据中甲的数据大于乙的数据的次数为
，求的分布列及数学期望．
（本小题满分10分）某地区100位居民的人均月用水量（单位：t）的频率分布直方图及频数分布表如下：
| 分组 |
频数 |
| [0，0．5） |
4 |
| [0．5，1） |
8 |
| [1，1．5） |
15 |
| [1．5，2） |
22 |
| [2，2．5） |
25 |
| [2．5，3） |
14 |
| [3，3．5） |
6 |
| [3．5，4） |
4 |
| [4，4．5] |
2 |
| 合计 |
100 |
（1）根据频率分布直方图估计这组数据的众数与平均数；
（2）当地政府制定了人均月用水量为3t的标准，若超出标准加倍收费，当地政府解释说，85%以上的居民不超出这个标准，这个解释对吗？为什么？
粤公网安备 44130202000953号
