高中数学空间向量的应用填空题

在棱长为1的正方体ABCD﹣A₁B₁C₁D₁中，过对角线BD₁的一个平面交AA₁于E，交CC₁于F，得四边形BFD₁E，给出下列结论：
①四边形BFD₁E有可能为梯形
②四边形BFD₁E有可能为菱形
③四边形BFD₁E在底面ABCD内的投影一定是正方形
④四边形BFD₁E有可能垂直于平面BB₁D₁D
⑤四边形BFD₁E面积的最小值为
其中正确的是　（请写出所有正确结论的序号）

如图，四边形ABCD和ADPQ均为正方形，它们所在的平面互相垂直，动点M在线段PQ上，E，F分别为AB，BC的中点，设异面直线EM与AF所成的角为，则的最大值为 ．

多面体上，位于同一条棱两端的顶点称为相邻的，如图，正方体的一个顶点在平面内，其余顶点在的同侧，正方体上与顶点相邻的三个顶点到的距离分别为1，2和4，是正方体的其余四个顶点中的一个，则到平面的距离可能是：
①3；②4；③5；④6；⑤7
以上结论正确的为______________。（写出所有正确结论的编号）

是异面直线，下面四个命题：
①过至少有一个平面平行于；
②过至少有一个平面垂直于；
③至多有一条直线与都垂直；
④至少有一个平面与都平行.
其中正确命题的个数是

若圆的圆心到直线（）的距离为，则.

如图所示，为正方体，给出以下五个结论：

①平面；
②平面；
③与底面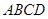所成角的正切值是；
④二面角的正切值是；
⑤过点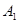且与异面直线和均成角的直线有2条．
其中，所有正确结论的序号为_______．

在正方形中，是的中点，是侧面内的动点且//平面，则与平面所成角的正切值得取值范围为.

如图，在空间直角坐标系中有棱长为a的正方体ABCD－A₁B₁C₁D₁，点M是线段DC₁上的动点，
则点M到直线AD₁距离的最小值是________．

已知侧棱长为2的正三棱锥如图所示，其侧面是顶角为的等腰三角形，一只蚂蚁从点出发，围绕棱锥侧面爬行两周后又回到点，则蚂蚁爬行的最短路程为_______．

如图， $\mathit{AE}\perp$平面 $\mathit{ABCD}$， $\mathit{CF}\parallel \mathit{AE},\mathit{AD}\parallel \mathit{BC}$， $\mathit{AD}\perp \mathit{AB},\mathit{AB}=\mathit{AD}=1,\mathit{AE}=\mathit{BC}=2$．

（Ⅰ）求证： $\mathit{BF}\parallel$平面 $\mathit{ADE}$；

（Ⅱ）求直线 $\mathit{CE}$与平面 $\mathit{BDE}$所成角的正弦值；

（Ⅲ）若二面角 $E-\mathit{BD}-F$的余弦值为 $\frac{1}{3}$，求线段 $\mathit{CF}$的长．

如图所示，在四边形中，,将四边形沿对角线折成四面体，使平面平面，则下列结论正确的是 ．

（1）；
（2）；
（3）与平面所成的角为；
（4）四面体的体积为．

已知直线与直线,若，则=_________；若则=___________________．

如图，四棱锥P-ABCD中，底面为菱形，且，．

（Ⅰ）求证：；
（Ⅱ）若，求二面角的余弦值．

长方体的各顶点都在球的球面上，其中．两点的球面距离记为，两点的球面距离记为，则的值为 ．

已知平面和直线，给出条件：
①；②；③；④；⑤．
（1）当满足条件时，有；（2）当满足条件时，有．