高中数学空间向量的应用填空题

在三棱锥中,底面,则点到平面的距离是_____________。

如图，在边长为的正方形SG₁G₂G₃中，E，F分别是G₁G₂，G₂G₃的中点，现沿SE，SF及EF把这个正方形折成一个三棱锥，使G₁，G₂，G₃三点重合，重合点记为G，则点G到平面SEF的距离为___________．

如图，是圆O的直径，是圆周上不同于的任意一点，平面，则四面体的四个面中，直角三角形的个数有个．

已知空间直角坐标系o﹣xyz中的点A的坐标为（1，1，1），平面α过点A且与直线OA垂直，动点P（x，y，z）是平面α内的任一点，则点P的坐标满足的条件是 ．

设表示两条直线，表示两个平面，现给出下列命题：
①若，则；
②若，则；
③若，则；
④若，则．
其中真命题是.（写出所有真命题的序号）

如图，四边形ABCD和ADPQ均为正方形，它们所在的平面互相垂直，动点M在线段PQ上，E，F分别为AB，BC的中点，设异面直线EM与AF所成的角为，则的最大值为 ．

是异面直线，下面四个命题：
①过至少有一个平面平行于；
②过至少有一个平面垂直于；
③至多有一条直线与都垂直；
④至少有一个平面与都平行.
其中正确命题的个数是

如图所示，为正方体，给出以下五个结论：

①平面；
②平面；
③与底面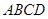所成角的正切值是；
④二面角的正切值是；
⑤过点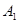且与异面直线和均成角的直线有2条．
其中，所有正确结论的序号为_______．

如图，在空间直角坐标系中有棱长为a的正方体ABCD－A₁B₁C₁D₁，点M是线段DC₁上的动点，
则点M到直线AD₁距离的最小值是________．

已知侧棱长为2的正三棱锥如图所示，其侧面是顶角为的等腰三角形，一只蚂蚁从点出发，围绕棱锥侧面爬行两周后又回到点，则蚂蚁爬行的最短路程为_______．

如图， $\mathit{AE}\perp$平面 $\mathit{ABCD}$， $\mathit{CF}\parallel \mathit{AE},\mathit{AD}\parallel \mathit{BC}$， $\mathit{AD}\perp \mathit{AB},\mathit{AB}=\mathit{AD}=1,\mathit{AE}=\mathit{BC}=2$．

（Ⅰ）求证： $\mathit{BF}\parallel$平面 $\mathit{ADE}$；

（Ⅱ）求直线 $\mathit{CE}$与平面 $\mathit{BDE}$所成角的正弦值；

（Ⅲ）若二面角 $E-\mathit{BD}-F$的余弦值为 $\frac{1}{3}$，求线段 $\mathit{CF}$的长．

如图所示，在四边形中，,将四边形沿对角线折成四面体，使平面平面，则下列结论正确的是 ．

（1）；
（2）；
（3）与平面所成的角为；
（4）四面体的体积为．

已知直线与直线,若，则=_________；若则=___________________．

如图，四棱锥P-ABCD中，底面为菱形，且，．

（Ⅰ）求证：；
（Ⅱ）若，求二面角的余弦值．

长方体的各顶点都在球的球面上，其中．两点的球面距离记为，两点的球面距离记为，则的值为 ．