已知直线l⊥平面α,直线m 平面β,有下列四个命题:①若α∥β,则l⊥m ;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.其中正确命题序号是.
平面β,有下列四个命题:①若α∥β,则l⊥m ;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.其中正确命题序号是.
将边长为2,锐角为 的菱形
的菱形 沿较短对角线
沿较短对角线 折成二面角
折成二面角 ,点
,点 分别为
分别为 的中点,给出下列四个命题:
的中点,给出下列四个命题:
① ;②
;② 是异面直线
是异面直线 与
与 的公垂线;③当二面角
的公垂线;③当二面角 是直二面角时,
是直二面角时, 与
与 间的距离为
间的距离为 ;④
;④ 垂直于截面
垂直于截面 .
.
其中正确的是(将正确命题的序号全填上).
如图1,已知点E、F、G分别是棱长为a的正方体ABCD-A1 B1Cl D1的棱AA1、BB1、DD1的中点,点M、N、P、Q分别在线段AG、 CF、BE、C1D1上运动,当以M、N、P、Q为顶点的三棱锥Q-PMN的俯视图是如图2所示的正方形时,则点P到QMN的距离为__________. 
三棱锥 中,
中, ,
,  ,D为AB的中点, ∠ABC=90°,则点D到面SBC的距离等于_____________.
,D为AB的中点, ∠ABC=90°,则点D到面SBC的距离等于_____________.
[2014·长春质检]如图,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为________.
设 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
①若 ,
, ,则
,则 ;
;
②若 ,
, ,
, ,
, ,则
,则 ;
;
③若 ,
, ,则
,则 ;
;
④若 ,
, ,
, ,
, ,则
,则
其中真命题的个数是.
设m,n,l为空间不重合的直线, 为空间不重合的平面,则下列命题中真命题的序号是.
为空间不重合的平面,则下列命题中真命题的序号是.
(1)m//l,n//l,则m//n;
(2)m l,n
l,n l,则m//n;
l,则m//n;
(3) ,则
,则 ;
;
(4) ,则
,则 ;
;
已知 是直线,
是直线, 是平面,下列命题中,正确的命题是.(填序号)
是平面,下列命题中,正确的命题是.(填序号)
①若 垂直于
垂直于 内两条直线,则
内两条直线,则 ;
;
②若 平行于
平行于 ,则
,则 内可有无数条直线与
内可有无数条直线与 平行;
平行;
③若m⊥n,n⊥l则m∥l;④若 ,则
,则 ;
;
(本小题满分14分)如图,在三棱柱 中,各个侧面均是边长为
中,各个侧面均是边长为 的正方形,
的正方形, 为线段
为线段 的中点.
的中点.
(Ⅰ)求证: ⊥平面
⊥平面 ;
;
(Ⅱ)求证:直线 ∥平面
∥平面 ;
;
(Ⅲ)设 为线段
为线段 上任意一点,在
上任意一点,在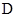
 内的平面区域(包括边界)是否存在点
内的平面区域(包括边界)是否存在点 ,使
,使
 ,并说明理由.
,并说明理由.
已知 是两条不同直线,
是两条不同直线, 、β、γ是三个不同平面.下列命题中正确的是 .
、β、γ是三个不同平面.下列命题中正确的是 .
(1).若 ⊥γ,β⊥γ,则
⊥γ,β⊥γ,则 //β
//β
(2).若 ⊥
⊥ ,
,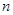 ⊥
⊥ ,则
,则 //
//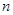
(3).若 //
// ,
,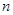 //
// ,则
,则 //
//
(4).若 //
// ,
, //β,则
//β,则 //β
//β
已知 ,
, 是空间中两条不同的直线,
是空间中两条不同的直线, ,
, ,
, 是空间中三个不同的平面,则下列命题正确的序号是.
是空间中三个不同的平面,则下列命题正确的序号是.
①若 ,
, ,则
,则 ;②若
;②若 ,
, ,则
,则 ;
;
③若 ,
, ,则
,则 ;④若
;④若 ,
, ,则
,则 .
.
已知直线l∥平面α,直线m Ìα,则直线l和m的位置关系是 .
(平行、相交、异面三种位置关系中选)
【改编】如图所示,已知三棱柱 的所有棱长均为1,且
的所有棱长均为1,且 底面
底面 ,则点
,则点 到平面
到平面 的距离为________.
的距离为________.