给出四个命题:
①平行于同一平面的两个不重合的平面平行;
②平行于同一直线的两个不重合的平面平行;
③垂直于同一平面的两个不重合的平面平行;
④垂直于同一直线的两个不重合的平面平行;
其中真命题的序号是________.
在正方体ABCD-A1B1C1D1中,下面结论中正确的是________(把正确结论的序号都填上).
①BD∥平面CB1D1;②AC1⊥平面CB1D1;③AC1与底面ABCD所成角的正切值是 .
.
对于四面体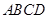 ,以下说法中,正确的序号为(多选、少选、选错均不得分).
,以下说法中,正确的序号为(多选、少选、选错均不得分).
①若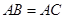 ,
,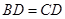 ,
,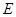 为
为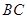 中点,则平面
中点,则平面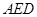 ⊥平面
⊥平面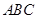 ;
;
②若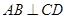 ,
,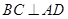 ,则
,则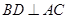 ;
;
③若所有棱长都相等,则该四面体的外接球与内切球的半径之比为2:1;
④若以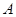 为端点的三条棱所在直线两两垂直,则
为端点的三条棱所在直线两两垂直,则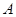 在平面
在平面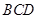 内的射影为
内的射影为 的垂心;
的垂心;
⑤分别作两组相对棱中点的连线,则所得的两条直线异面。
如图,长方体 中,
中, 是边长为
是边长为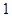 的正方形,
的正方形, 与平面
与平面 所成的角为
所成的角为 ,则棱
,则棱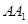 的长为_______;二面角
的长为_______;二面角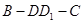 的大小为_______.
的大小为_______.
如图,正四棱柱ABCD—A1B1C1D1中,AA1=2AB=4,点E在C1C上,且C1E=3EC.
(1)证明A1C⊥平面BED;
(2)求二面角A1-DE-B的余弦值.
在四面体ABCD中,有如下结论:
①若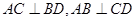 ,则
,则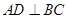 ;
;
②若 分别是
分别是 的中点,则
的中点,则 的大小等于异面直线
的大小等于异面直线 与
与 所成角的大小;
所成角的大小;
③若点 是四面体
是四面体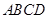 外接球的球心,则
外接球的球心,则 在面
在面 上的射影为
上的射影为 的外心;
的外心;
④若四个面是全等的三角形,则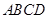 为正四面体.
为正四面体.
其中所有正确结论的序号是.
如图所示,在正方体 中,点
中,点 是棱
是棱 上的一个动点,平面
上的一个动点,平面 交棱
交棱 于点
于点 .给出下列四个结论:
.给出下列四个结论:
①存在点 ,使得
,使得 //平面
//平面 ;
;
②存在点 ,使得
,使得 平面
平面 ;
;
③对于任意的点 ,平面
,平面 平面
平面 ;
;
④对于任意的点 ,四棱锥
,四棱锥 的体积均不变.
的体积均不变.
其中,所有正确结论的序号是___________.
如图,在边长为 的正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个三棱锥,使G1,G2,G3三点重合,重合点记为G,则点G到平面SEF的距离为___________.
的正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个三棱锥,使G1,G2,G3三点重合,重合点记为G,则点G到平面SEF的距离为___________.
如图, 平面 , , .
(Ⅰ)求证: 平面 ;
(Ⅱ)求直线 与平面 所成角的正弦值;
(Ⅲ)若二面角 的余弦值为 ,求线段 的长.

如图所示,在四边形 中,
中, ,将四边形
,将四边形 沿对角线
沿对角线 折成四面体
折成四面体 ,使平面
,使平面 平面
平面 ,则下列结论正确的是 .
,则下列结论正确的是 .
(1) ;
;
(2) ;
;
(3) 与平面
与平面 所成的角为
所成的角为 ;
;
(4)四面体 的体积为
的体积为 .
.
长方体 的各顶点都在球
的各顶点都在球 的球面上,其中
的球面上,其中 .
. 两点的球面距离记为
两点的球面距离记为 ,
, 两点的球面距离记为
两点的球面距离记为 ,则
,则 的值为 .
的值为 .