在棱长为1的正方体ABCD﹣A1B1C1D1中，过对角线BD1的一个平面交AA1于E，交CC1于F，得四边形BFD1E，给出下列结论：
①四边形BFD1E有可能为梯形
②四边形BFD1E有可能为菱形
③四边形BFD1E在底面ABCD内的投影一定是正方形
④四边形BFD1E有可能垂直于平面BB1D1D
⑤四边形BFD1E面积的最小值为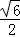
其中正确的是 （请写出所有正确结论的序号）
中，
为
,则数列
的最大项为第____项．
，满足
,
，则
的最大值是__________．
中，角
所对应的边分别为
，已知
，则
=______．
的图象与直线
有且只有一个交点，则实数
的取值范围是．
若
，则实数
的值等于．推荐套卷
在棱长为1的正方体ABCD﹣A1B1C1D1中，过对角线BD1的一个平面交AA1于E，交CC1于F，得四边形BFD1E，给出下列结论：
①四边形BFD1E有可能为梯形
②四边形BFD1E有可能为菱形
③四边形BFD1E在底面ABCD内的投影一定是正方形
④四边形BFD1E有可能垂直于平面BB1D1D
⑤四边形BFD1E面积的最小值为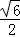
其中正确的是 （请写出所有正确结论的序号）
粤公网安备 44130202000953号