如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形, ,
, 为
为 的中点.
的中点.
(1)若 ,求证:平面
,求证:平面 平面
平面 ;
;
(2)设点 是线段
是线段 上的一点,
上的一点, ,且
,且 平面
平面 .
.
(1)求实数 的值;
的值;
(2)若 ,且平面
,且平面 平面
平面 ,求二面角
,求二面角 的大小.
的大小.
如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
(Ⅰ)判定AE与PD是否垂直,并说明理由;
(Ⅱ)若PA=2,求二面角E-AF-C的余弦值.
如图,在正方体 的棱长为
的棱长为 ,
, 为棱
为棱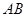 上的一动点.
上的一动点.

(1)若 为棱
为棱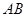 的中点,
的中点,
①求四棱锥 的体积
的体积
②求证:面 面
面
(2)若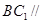 面
面 ,求证:
,求证: 为棱
为棱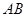 的中点.
的中点.
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60o,PA=AB, .
.
(1)求证:证明:BD⊥平面PAC;
(2)求PC与平面PAB所成角的正切值.
如图所示,在四棱锥PABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.

(1)证明:PC⊥AD;
(2)求二面角A-PC-D的正弦值.
如图, 是圆台上底面圆
是圆台上底面圆 的直径,
的直径, 是圆
是圆 上不同于
上不同于 的一点,
的一点, 是下底面圆
是下底面圆 上一点,过
上一点,过 的截面垂直与下底面,
的截面垂直与下底面, 为
为 的中点,又
的中点,又 .
.
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.