如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,E为侧棱PA的中点.
(1)求证:PC //平面BDE;
(2)若PC⊥PA,PD=AD,求证:平面BDE⊥平面PAB.
如图,矩形ABCD所在的平面与三角形CDE所在的平面交于CD, AE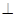 平面CDE.
平面CDE.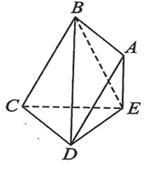
求证:(1)AB//平面CDE;
(2)CD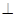 平面ADE.
平面ADE.
如图,四棱锥 ,平面
,平面 ⊥平面
⊥平面 ,△
,△ 是边长为2的等边三角形,底面
是边长为2的等边三角形,底面 是矩形,且
是矩形,且 .
.
(1)若点 是
是 的中点,求证:
的中点,求证: 平面
平面 ;
;
(2)若 为
为 上任意一点,试问点
上任意一点,试问点 在线段
在线段 上什么位置时,
上什么位置时, ⊥
⊥ ;
;
(3)若点 是
是 的中点,求
的中点,求 .
.
如图,在四棱锥 中,底面
中,底面 为直角梯形,
为直角梯形, ,
, ,平面
,平面 底面
底面 ,
, 为
为 的中点,
的中点, 是棱
是棱 上的点,
上的点, ,
, ,
, .
.
(1)求证:平面 平面
平面 ;
;
(2)若 为棱
为棱 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)若二面角 大小为
大小为 ,求
,求 的长.
的长.
如图,四棱锥P—ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,点E是PB的中点,点F是EB的中点.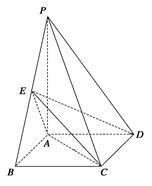
(Ⅰ) 求证: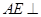 平面
平面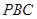 ;
;
(Ⅱ) 求证: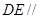 平面
平面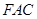 .
.
如图所示的几何体中EA 平面ABC,BD
平面ABC,BD 平面ABC,AC=BC=BD=2AE=
平面ABC,AC=BC=BD=2AE= ,M是AB的中点
,M是AB的中点
(1)求证:CM  EM;
EM;
(2)求MC与面EAC所成的角.
四棱锥P﹣ABCD中,底面ABCD是边长为8的菱形,∠BAD= ,若PA=PD=5,平面PAD⊥平面ABCD.
,若PA=PD=5,平面PAD⊥平面ABCD.
(1)求四棱锥P﹣ABCD的体积;
(2)求证:AD⊥PB.