已知映射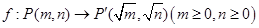 .设点
.设点 ,
,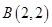 ,点
,点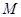 是线段
是线段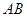 上一动点,
上一动点,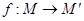 .当点
.当点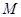 在线段
在线段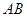 上从点
上从点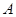 开始运动到点
开始运动到点 结束时,点
结束时,点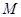 的对应点
的对应点 所经过的路线长度为()
所经过的路线长度为()
A. |
B.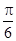 |
C. |
D.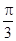 |
已知函数 ,且方程
,且方程 有两个实根
有两个实根
(1)求函数 的解析式;
的解析式;
(2)设 ,解关于
,解关于 的不等式
的不等式 .
.
如图所示,直线 ⊥
⊥ 轴,从原点开始向右平行移动到
轴,从原点开始向右平行移动到 处停止,它截△AOB所得左侧图形的面积为S,它与x轴的交点为
处停止,它截△AOB所得左侧图形的面积为S,它与x轴的交点为 .
. 
(1)求函数 的解析式;
的解析式;
(2)解不等式 .
.
已知二次函数 ,满足
,满足 ,且方程
,且方程 有两个相等的实根.
有两个相等的实根.
(1)求函数 的解析式;
的解析式;
(2)当
 时,求函数
时,求函数 的最小值
的最小值 的表达式.
的表达式.
某位股民购进某只股票,在接下来的交易时间内,他的这只股票先经历了n次涨停(每次上涨10%),又经历了n次跌停(每次下跌10%),则该股民这只股票的盈亏情况(不考虑其它费用)是
| A.略有盈利 |
| B.略有亏损 |
| C.没有盈利也没有亏损 |
| D.无法判断盈亏情况 |
设 为二次函数,且
为二次函数,且 ,
, .
.
(1)求 的解析式;
的解析式;
(2)设 ,若函数
,若函数 在实数
在实数 上没有零点,求
上没有零点,求 的取值范围.
的取值范围.
(本小题满分12分)设 为定义在R上的偶函数,当
为定义在R上的偶函数,当 时,
时, .
.
(1)求函数 在R上的解析式;
在R上的解析式;
(2)在直角坐标系中画出函数 的图象;
的图象;
(3)若方程 -k=0有四个解,求实数k的取值范围.
-k=0有四个解,求实数k的取值范围.
(本小题满分15分)已知函数 (
( 且
且 ).
).
(Ⅰ)若 ,试求
,试求 的解析式;
的解析式;
(Ⅱ)令 ,若
,若 ,又
,又 的图像在
的图像在 轴上截得的弦的长度为
轴上截得的弦的长度为 ,且
,且 ,试比较
,试比较 、
、 的大小.
的大小.