高中数学数列综合解答题

已知正项等比数列，首项，前项和为，且，，成等差数列．
（1）求数列的通项公式；
（2）求数列的前项和．

已知是等差数列，满足，数列满足，且为等比数列．
（1）求数列的通项公式；
（2）求数列的前n项和．

设等差数列{a_n}的公差为d，点(a_n，b_n)在函数f (x)＝2^x的图象上(n∈N^*)．
（Ⅰ）证明：数列{b_n}为等比数列；
（Ⅱ）若a₁＝1，直线y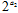＝(ln2)(x－a₂)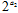＋在x轴上的截距为2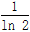－，求数列{a_nb}的前n项和S_n.

能否为同一等差数列中的三项？说明理由．

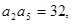
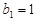已知等比数列是递增数列，，数列满足，且（）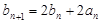
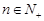（1）证明：数列是等差数列；
（2）若对任意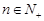，不等式总成立，求实数的最大值．

设数列的前项和满足且成等差数列．
（Ⅰ）求数列的通项公式；
（Ⅱ）设数列的前项和为，求．

为公差不为0的等差数列，，且成等比数列．
（1）求数列的通项公式；
（2）若数列的前项n和为，求数列的前项n和．

已知数列满足,．
（1）求证：数列是等比数列，并求出通项公式；
（2）若数列设是数列的前项和，求证：．

等差数列中,
（1）求的通项公式；
（2）设

等差数列中,
（1）求的通项公式;
（2）设

已知为等差数列的前项和,且．
（Ⅰ）求数列的通项公式；
（Ⅱ）求数列的前项和公式．

公差不为零的等差数列{a_n}中，a₁、a₂、a₅成等比数列，且该数列的前10项和为100．
（1）求数列{a_n}的通项公式；
（2）若b_n=a_n﹣10，求数列{b_n}的前n项和T_n的最小值．

公差不为零的等差数列{a_n}中，a₁、a₂、a₅成等比数列，且该数列的前10项和为100．
（1）求数列{a_n}的通项公式；
（2）若b_n=a_n﹣10，求数列{b_n}的前n项和T_n的最小值．

已知{a_n}是正项数列，a₁=1，且点（，a_n+1）（n∈N^*）在函数y=x²+1的图象上．
（1）求数列{a_n}的通项公式；
（2）若列数{b_n}满足b₁=1，b_n+1=b_n+2，求证：b_nb_n+2＜b．

在正项数列{a_n}中，a₁=1，点A_n（）在曲线y²﹣x²=1上，数列{b_n}中，点（b_n，T_n）在直线y=﹣x+1上，其中T_n是数列{b_n}的前n项和．
（1）求数列{a_n}，{b_n}的通项公式a_n，b_n；
（2）若c_n=a_n•b_n，数列{c_n}的前n项和S_n．