如图1,在平面直角坐标系 内,已知点
内,已知点 ,
, ,
, ,
, ,记线段
,记线段 为
为 ,线段
,线段 为
为 ,点
,点 是坐标系内一点.给出如下定义:若存在过点
是坐标系内一点.给出如下定义:若存在过点 的直线l与
的直线l与 ,
, 都有公共点,则称点
都有公共点,则称点 是
是 联络点.
联络点.
例如,点
 是
是 联络点.
联络点.
(1)以下各点中,__________________是 联络点(填出所有正确的序号);
联络点(填出所有正确的序号);
① ;②
;②  ;③
;③ .
.
(2)直接在图1中画出所有 联络点所组成的区域,用阴影部分表示;
联络点所组成的区域,用阴影部分表示;
(3)已知点M在y轴上,以M为圆心,r为半径画圆,⊙M上只有一个点为 联络点,①若
联络点,①若 ,求点M的纵坐标;
,求点M的纵坐标;
②求 的取值范围.
的取值范围.
给出如下规定:两个图形G1和G2,点P为G1上任一点,点Q为G2上任一点,如果线段PQ的长度存在最小值,就称该最小值为两个图形G1和G2之间的距离.在平面直角坐标系xOy中,O为坐标原点.
(1)点A的坐标为 ,则点
,则点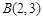 和射线OA之间的距离为________,点
和射线OA之间的距离为________,点 和射线OA之间的距离为________;
和射线OA之间的距离为________;
(2)如果直线 和双曲线
和双曲线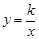 之间的距离为
之间的距离为 ,那么k= ;(可在图1中进行研究)
,那么k= ;(可在图1中进行研究)
(3)点E的坐标为(1, ),将射线OE绕原点O逆时针旋转60°,得到射线OF,在坐标平面内所有和射线OE,OF之间的距离相等的点所组成的图形记为图形M.
),将射线OE绕原点O逆时针旋转60°,得到射线OF,在坐标平面内所有和射线OE,OF之间的距离相等的点所组成的图形记为图形M.
①请在图2中画出图形M,并描述图形M的组成部分;(若涉及平面中某个区域时可以用阴影表示)
②将射线OE,OF组成的图形记为图形W,抛物线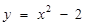 与图形M的公共部分记为图形N,请直接写出图形W和图形N之间的距离.
与图形M的公共部分记为图形N,请直接写出图形W和图形N之间的距离.

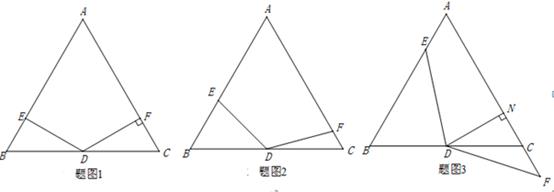
在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证: ;
;
(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交与点F,作DN⊥AC于点N,若DN=FN,求证: .
.
(本小题满分13分)已知函数 满足
满足 ,且当
,且当 时,
时, ,当
,当 时,
时, 的最大值为
的最大值为 .
.
(1)求实数a的值;
(2)设 ,函数
,函数 ,
, .若对任意
.若对任意 ,总存在
,总存在 ,使
,使 ,求实数b的取值范围.
,求实数b的取值范围.
(本小题满分13分)已知函数 ..
..
(Ⅰ)若 ,求函数
,求函数 的最大值;
的最大值;
(Ⅱ)令 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅲ)若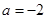 ,正实数
,正实数 满足
满足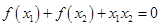 ,证明
,证明 .
.
如图,一辆汽车在一条水平的公路上向正西行驶,到 处时测得公路北侧一山顶D在西偏北
处时测得公路北侧一山顶D在西偏北 的方向上,行驶600m后到达
的方向上,行驶600m后到达 处,测得此山顶在西偏北
处,测得此山顶在西偏北 的方向上,仰角为
的方向上,仰角为 ,则此山的高度
,则此山的高度 _________m.
_________m. 
如图,已知椭圆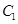 与
与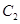 的中心在坐标原点
的中心在坐标原点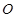 ,长轴均为
,长轴均为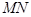 且在
且在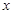 轴上,短轴长分别为
轴上,短轴长分别为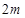 ,
,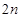
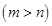 ,过原点且不与
,过原点且不与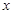 轴重合的直线
轴重合的直线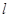 与
与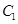 ,
,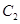 的四个交点按纵坐标从大到小依次为
的四个交点按纵坐标从大到小依次为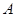 、
、 、
、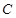 、
、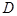 .记
.记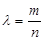 ,
,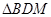 和
和 的面积分别为
的面积分别为 和
和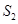 .
.
(1)当直线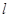 与
与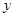 轴重合时,若
轴重合时,若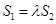 ,求
,求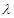 的值;;
的值;;
(2)设直线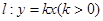 ,若
,若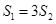 ,证明:
,证明: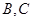 是线段
是线段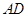 的四等分点
的四等分点
(3)当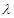 变化时,是否存在与坐标轴不重合的直线
变化时,是否存在与坐标轴不重合的直线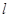 ,使得
,使得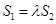 ?并说明理由.
?并说明理由.
(本小题满分12分)如图,在四棱锥P—ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.
(Ⅰ)若PA=PD,求证:平面POB⊥平面PAD;
(Ⅱ)若平面PAD⊥平面ABCD,且PA=PD=AD=2,试问在线段PC上是否存在点M,使二面角M—BO—C的大小为60°,如存在,求 的值,如不存在,说明理由.
的值,如不存在,说明理由.
(本小题满分16分)如图,在平面直角坐标系 中,椭圆
中,椭圆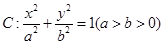 的离心率为
的离心率为 ,直线
,直线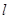 与
与 轴交于点
轴交于点 ,与椭圆
,与椭圆 交于
交于 、
、 两点.当直线
两点.当直线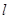 垂直于
垂直于 轴且点
轴且点 为椭圆
为椭圆 的右焦点时, 弦
的右焦点时, 弦 的长为
的长为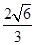 .
.
(1)求椭圆 的方程;
的方程;
(2)若点 的坐标为
的坐标为 ,点
,点 在第一象限且横坐标为
在第一象限且横坐标为 ,连结点
,连结点 与原点
与原点 的直线交椭圆
的直线交椭圆 于另一点
于另一点 ,求
,求 的面积;
的面积;
(3)是否存在点 ,使得
,使得 为定值?若存在,请指出点
为定值?若存在,请指出点 的坐标,并求出该定值;若不存在,请说明理由.
的坐标,并求出该定值;若不存在,请说明理由.
(本小题满分14分)已知函数 ,其中
,其中 为实数.
为实数.
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ) 当 时,若函数
时,若函数 对定义域内的任意
对定义域内的任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(Ⅲ)证明,对于任意的正整数 ,不等式
,不等式 恒成立.
恒成立.
已知曲线 在
在 处的切线与直线
处的切线与直线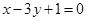 垂直.
垂直.
(Ⅰ)求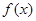 解析式;
解析式;
(Ⅱ)求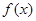 的单调区间并画出
的单调区间并画出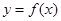 的大致图象;
的大致图象;
(Ⅲ)已知函数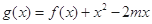 ,若对任意
,若对任意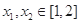 ,总有
,总有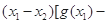
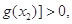 求实数
求实数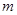 的取值范围.
的取值范围.
(本小题满分16分)设函数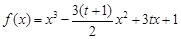 (
(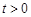 ).
).
(1)若 ,求函数
,求函数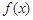 的极大值;
的极大值;
(2)若存在 ,使得
,使得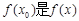 在区间[0,2]上的最小值,求实数t的取值范围;
在区间[0,2]上的最小值,求实数t的取值范围;
(3)若 (e
(e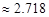 )对任意的
)对任意的 恒成立时m的最大值为
恒成立时m的最大值为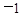 ,求实数t的取值范围.
,求实数t的取值范围.
(本小题满分16分)已知点 为椭圆
为椭圆 上的任意一点(长轴的端点除外),
上的任意一点(长轴的端点除外), 、
、 分别为左、右焦点,其中a,b为常数.
分别为左、右焦点,其中a,b为常数.

(1)若点P在椭圆的短轴端点位置时, 为直角三角形,求椭圆的离心率.
为直角三角形,求椭圆的离心率.
(2)求证:直线 为椭圆在点P处的切线方程;
为椭圆在点P处的切线方程;
(3)过椭圆的右准线上任意一点R作椭圆的两条切线,切点分别为S、T.请判断直线ST是否经过定点?若经过定点,求出定点坐标,若不经过定点,请说明理由.
(本小题满分16分)某仓库为了保持库内温度,四周墙上装有如图所示的通风设施,该设施的下部是等边三角形ABC,其中AB=2米,上部是半圆,点E为AB的中点.△EMN是通风窗,(其余部分不通风)MN是可以沿设施的边框上下滑动且保持与AB平行的伸缩杆(MN和AB不重合).
(1)设MN与C之间的距离为x米,试将△EMN的面积S表示成 的函数
的函数 ;
;
(2)当MN与C之间的距离为多少时,△EMN面积最大?并求出最大值.