已知数列 是公差不为0的等差数列,a1=2且a2,a3,a4+1成等比数列。
是公差不为0的等差数列,a1=2且a2,a3,a4+1成等比数列。
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和
已知椭圆C: 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切。
相切。
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C交于两点A和B,设P为椭圆上一点,且满足
 ·
· (O为坐标原点),当
(O为坐标原点),当 时,求实数t取值范围。
时,求实数t取值范围。
如图1,在△ABC中,BC=3,AC=6,∠C=90°,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2。
(1)求证:BC⊥平面A1DC;
(2)若CD=2,求BE与平面A1BC所成角的正弦值。
已知数列 的前
的前 项和为
项和为 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 log2an+1 ,求数列
log2an+1 ,求数列 的前
的前 项和
项和 。
。
.给出下列命题:
① 已知线性回归方程 ,当变量
,当变量 增加2个单位,其预报值平均增加4个单位;
增加2个单位,其预报值平均增加4个单位;
② 在进制计算中, ;
;
③ 若 ,且
,且 ,则
,则 ;
;
④ “ ”是“函数
”是“函数 的最小正周期为4”的充要条件;
的最小正周期为4”的充要条件;
⑤ 设函数 的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是 个。
的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是 个。
在平面直角坐标系中,若 ,且
,且 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)已知定点 ,若斜率为
,若斜率为 的直线
的直线 过点
过点 并与轨迹
并与轨迹 交于不同的两点
交于不同的两点 ,且对于轨迹
,且对于轨迹 上任意一点
上任意一点 ,都存在
,都存在 ,使得
,使得 成立,试求出满足条件的实数
成立,试求出满足条件的实数 的值.
的值.
如图,椭圆 经过点
经过点 ,离心率
,离心率 ,直线
,直线 的方程为
的方程为 .
.
(1)求椭圆 的方程;
的方程;
(2) 是经过右焦点
是经过右焦点 的任一弦(不经过点
的任一弦(不经过点 ),设直线
),设直线 与直线
与直线 相交于点
相交于点 ,记
,记 的斜率分别为
的斜率分别为 .问:是否存在常数
.问:是否存在常数 ,使得
,使得 ?若存在,求
?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
以下四个关于圆锥曲线的命题中:①设 为两个定点,
为两个定点, 为非零常数,
为非零常数, ,则动点
,则动点 的轨迹为双曲线;②过定圆
的轨迹为双曲线;②过定圆 上一定点
上一定点 作圆的动点弦
作圆的动点弦 ,
, 为坐标原点,若
为坐标原点,若 则动点
则动点 的轨迹为圆;③设
的轨迹为圆;③设 是
是 的一内角,且
的一内角,且 ,则
,则 表示焦点在
表示焦点在 轴上的双曲线;④已知两定点
轴上的双曲线;④已知两定点 和一动点
和一动点 ,若
,若 ,则点
,则点 的轨迹关于原点对称.
的轨迹关于原点对称.
其中真命题的序号为 (写出所有真命题的序号).
已知中心在原点的双曲线 的右焦点为
的右焦点为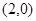 ,实轴长
,实轴长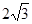 .
.
(1)求双曲线的方程
(2)若直线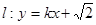 与双曲线恒有两个不同的交点
与双曲线恒有两个不同的交点 ,且
,且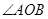 为锐角(其中
为锐角(其中 为原点),求
为原点),求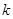 的取值范围.
的取值范围.
是否同时存在满足下列条件的双曲线,若存在,求出其方程,若不存在,说明理由.
(1)焦点在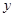 轴上的双曲线渐近线方程为
轴上的双曲线渐近线方程为 ;
;
(2)点 到双曲线上动点
到双曲线上动点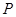 的距离最小值为
的距离最小值为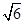 .
.
以下四个关于圆锥曲线的命题中:①设 为两个定点,
为两个定点, 为非零常数,
为非零常数, ,则动点
,则动点 的轨迹为双曲线;②过定圆
的轨迹为双曲线;②过定圆 上一定点
上一定点 作圆的动点弦
作圆的动点弦 ,
, 为坐标原点,若
为坐标原点,若 则动点
则动点 的轨迹为圆;③
的轨迹为圆;③ ,则双曲线
,则双曲线 与
与 的离心率相同;④已知两定点
的离心率相同;④已知两定点 和一动点
和一动点 ,若
,若 ,则点
,则点 的轨迹关于原点对称.
的轨迹关于原点对称.
其中真命题的序号为 (写出所有真命题的序号).