高中数学试题

一个圆柱形圆木的底面半径为1m，长为10m，将此圆木沿轴所在的平面剖成两个部分．现要把其中一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形（如图所示，其中O为圆心，在半圆上），设，木梁的体积为V（单位：m³），表面积为S（单位：m²）．

（1）求V关于θ的函数表达式；
（2）求的值，使体积V最大；
（3）问当木梁的体积V最大时，其表面积S是否也最大？请说明理由．

如图，在三棱柱中，侧面为菱形， 且，，是的中点．

（1）求证：平面平面；
（2）求证：∥平面．

在平面直角坐标系中，已知点在圆内，动直线过点且交圆于两点，若△ABC的面积的最大值为，则实数的取值范围为      ．

已知椭圆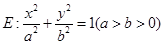的左、右焦点分别为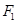、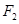， 焦距为2，过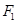作垂直于椭圆长轴的弦长为3
（1）求椭圆的方程；
（2）若过点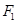的动直线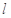交椭圆于A、B两点，判断是否存在直线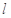使得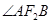为钝角，若存在，求出直线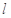的斜率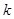的取值范围

如图，△ABC内接于圆O,AB是圆O的直径，四边形DCBE为平行四边形，DC平面ABC,,

（1）证明：平面ACD平面ADE；
（2）记，表示三棱锥A－CBE的体积，求函数的解析式及最大值

在数列中，为常数，，且成公比不等于1的等比数列
（1）求的值；
（2）设，求数列的前项和 

如图，用一边长为的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将表面积为的鸡蛋（视为球体）放入其中，蛋巢形状保持不变, 则鸡蛋中心（球心）与蛋巢底面的距离为

A．

B．

C．

D．

已知函数，若函数在上有两个零点，则的取值范围是

A．

B．

C．

D．

已知椭圆的两焦点在轴上, 且两焦点与短轴的一个顶点的连线构成斜边长为2的等腰直角三角形
（1）求椭圆的方程；
（2）过点的动直线交椭圆C于A、B两点，试问：在坐标平面上是否存在一个定点Q，使得以AB为直径的圆恒过点Q?若存在求出点Q的坐标；若不存在，请说明理由

如图1，在Rt中，， D、E分别是上的点，且，将沿折起到的位置，使，如图2．

（1）求证：平面平面；
（2）若，求与平面所成角的余弦值；
（3）当点在何处时，的长度最小，并求出最小值．

在数列中，为常数，，且成公比不等于1的等比数列
（1）求的值；
（2）设，求数列的前项和 

已知函数,且函数恰有3个不同的零点,则实数的取值范围是（     ）

A．

B．

C．

D．

已知双曲线＝1的离心率为2，焦点到渐近线的距离等于，过右焦点F₂的直线l交双曲线于A、B两点，F₁为左焦点．
(1)求双曲线的方程；
(2)若△F₁AB的面积等于6，求直线l的方程．

已知椭圆＝1(a>b>0)的离心率e＝，连结椭圆的四个顶点得到的菱形的面积为4.
(1)求椭圆的方程；
(2)设直线l与椭圆相交于不同的两点A，B.已知点A的坐标为(－a，0)．若|AB|＝，求直线l的倾斜角．

已知椭圆C：＝1(a>b>0)经过点M(－2，－1)，离心率为.过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
(1)求椭圆C的方程；
(2)试判断直线PQ的斜率是否为定值，证明你的结论．