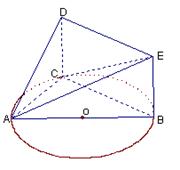
如图，△ABC内接于圆O,AB是圆O的直径，四边形DCBE为平行四边形，DC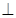
平面ABC,
,
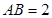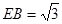
（1）证明：平面ACD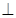平面ADE；
（2）记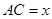
，
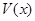表示三棱锥A－CBE的体积，求函数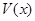的解析式及最大值
，
；
。
，
，
， 
，
，求集合
，
，
，求
上
对一切实数x恒成立，求实数a的取值范围。
中，已知
．
；（2）若
AB=4 ,求相关知识点
推荐套卷
如图，△ABC内接于圆O,AB是圆O的直径，四边形DCBE为平行四边形，DC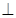平面ABC,,
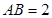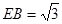
（1）证明：平面ACD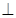平面ADE；
（2）记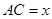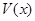，表示三棱锥A－CBE的体积，求函数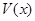的解析式及最大值
粤公网安备 44130202000953号