(本小题满分14分)某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图).
| 分组 |
频数 |
频率 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求 ,
, 的值.
的值.
(2)求在未来连续3天里,有连续2天的日销售量都高于100个且另1天的日销售量不高于50
个的概率;
(3)用 表示在未来3天里日销售量高于100个的天数,求随机变量
表示在未来3天里日销售量高于100个的天数,求随机变量 的分布列和数学期望.
的分布列和数学期望.
推荐套卷
 的函数
的函数 是奇函数.
是奇函数. 的值;
的值; 的单调性,并证明.
的单调性,并证明. ,
, .
. ,使得
,使得 ,求
,求 的取值范围;
的取值范围; ,求
,求 ,求
,求 的值;
的值; ,且
,且 ,求
,求 的值.
的值.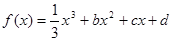 ,设曲线
,设曲线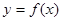 在与
在与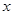 轴交点处的切线为
轴交点处的切线为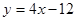 ,
,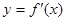 为
为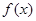 的导函数,满足
的导函数,满足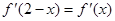 .
.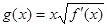 ,
,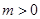 ,求函数
,求函数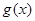 在
在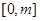 上的最大值;
上的最大值;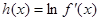 ,若对于一切
,若对于一切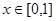 ,不等式
,不等式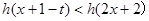 恒成立,求实数
恒成立,求实数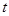 的取值范围.
的取值范围.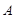 是同时符合以下性质的函数
是同时符合以下性质的函数 组成的集合:
组成的集合: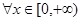 ,都有
,都有 ;②
;②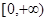 上是减函数.
上是减函数.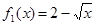 和
和 (
( )是否属于集合
)是否属于集合 ,若不等式
,若不等式 对任意的
对任意的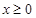 总成立,求实数
总成立,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号