吉林省延边州高考复习质量检测文科数学试卷
 表示不同直线,M表示平面,给出四个命题:①若
表示不同直线,M表示平面,给出四个命题:①若 ∥M,
∥M, ∥M,则
∥M,则 ∥
∥ 或
或 相交或
相交或 异面;②若
异面;②若 M,
M, ∥
∥ ,则
,则 ∥M;③
∥M;③ ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ∥
∥ ;④
;④ ⊥M,
⊥M, ⊥M,则
⊥M,则 ∥
∥ ,其中正确命题为
,其中正确命题为
| A.①④ | B.②③ | C.③④ | D.①② |
设函数 ,则下列结论正确的是
,则下列结论正确的是
A. 的图像关于直线 的图像关于直线 对称 对称 |
B. 的图像关于点 的图像关于点 对称 对称 |
C. 的最小正周期为 的最小正周期为 |
D. 在 在 上为增函数 上为增函数 |
已知正数a,b满足4a+b=30,使得 取最小值的实数对(a,b)是
取最小值的实数对(a,b)是
| A.(5,10) | B.(6,6) | C.(10,5) | D.(7,2) |
关于x的方程ex-1-|kx|=0(其中e=2.71828…是自然对数的底数)的有三个不同实根,则k的取值范围是
| A.{-2,0,2} | B.(1,+∞) | C.{k|k>e} | D.{k|k2>1} |
设△ABC的三个内角A、B、C所对的三边分别为a,b,c,若△ABC的面积为S=a2-(b-c)2,则 = .
= .
给出下列命题:
① 已知线性回归方程 ,当变量
,当变量 增加2个单位,其预报值平均增加4个单位;
增加2个单位,其预报值平均增加4个单位;
② 在进制计算中, ;
;
③ 若 ,且
,且 ,则
,则 ;
;
④ “ ”是“函数
”是“函数 的最小正周期为4”的充要条件;
的最小正周期为4”的充要条件;
⑤ 设函数 的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是 个。
的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是 个。
已知数列 是公差不为0的等差数列,a1=2且a2,a3,a4+1成等比数列。
是公差不为0的等差数列,a1=2且a2,a3,a4+1成等比数列。
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和
某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间。按年龄分组:第1组 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。
| 区间 |
 |
 |
 |
 |
 |
| 人数 |
 |
a |
b |
|
|
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组中抽取的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1 人在第3组的概率。
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2。
(1)求证:CE∥平面PAB;
(2)求四面体PACE的体积.
已知椭圆 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率 ,直线
,直线 交椭圆于M,N两点。
交椭圆于M,N两点。
(1)若直线 的方程为
的方程为 ,求弦MN的长;
,求弦MN的长;
(2)如果△BMN的重心恰好为椭圆的右焦点F,求直线 方程的一般式。
方程的一般式。
如图,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5。
求:(1)⊙O的半径;
(2)s1n∠BAP的值。
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中 轴的正半轴重合,且两坐标系有相同的长度单位,圆C的参数方程为
轴的正半轴重合,且两坐标系有相同的长度单位,圆C的参数方程为 (
( 为参数),点Q的极坐标为
为参数),点Q的极坐标为 。
。
(1)化圆C的参数方程为极坐标方程;
(2)直线 过点Q且与圆C交于M,N两点,求当弦MN的长度为最小时,直线
过点Q且与圆C交于M,N两点,求当弦MN的长度为最小时,直线 的直角坐标方程。
的直角坐标方程。
 ,集合
,集合 ,则
,则




 +i2的虚部是
+i2的虚部是 ”是“
”是“ ”的
”的









 的一个焦点在圆
的一个焦点在圆 上,则双曲线的渐近线方程为
上,则双曲线的渐近线方程为



 在区间
在区间 上满足
上满足 ,则满足
,则满足 的
的 的取值范围是
的取值范围是



 ,则目标函数
,则目标函数 的最小值为 。
的最小值为 。 ,且
,且 ∥
∥ ,则实数
,则实数 的值是 。
的值是 。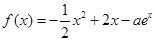 。
。 ,求
,求 在
在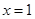 处的切线方程;
处的切线方程; 的取值范围。
的取值范围。 ,
, 。
。 的解集;
的解集; 有解,求实数
有解,求实数 的取值范围。
的取值范围。 粤公网安备 44130202000953号
粤公网安备 44130202000953号