P为椭圆 =1上一点,M、N分别是圆(x+3)2+y2=4和(x-3)2+y2=1上的点,则|PM|+|PN|的取值范围是 ( )
=1上一点,M、N分别是圆(x+3)2+y2=4和(x-3)2+y2=1上的点,则|PM|+|PN|的取值范围是 ( )
A.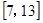 |
B.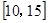 |
C. |
D.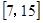 |
在平面直角坐标系xOy中,曲线y=x2-2x-3与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若直线x+y+a=0与圆C交于A,B两点,且AB=2,求实数a的值.
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AA1=3,ÐBAA1=60°,E为棱C1D1的中点,则 .
.

如图,在三棱柱ABC-A1B1C1中,C1C⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.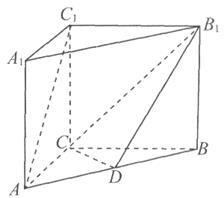
(1)求证:AC1∥平面CDB1;
(2)求四面体B1C1CD的体积.
已知抛物线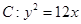 ,点
,点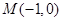 ,过
,过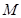 的直线
的直线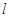 交抛物线
交抛物线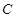 于
于 两点.
两点.
(1)若线段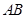 中点的横坐标等于
中点的横坐标等于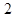 ,求直线
,求直线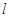 的斜率;
的斜率;
(2)设点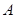 关于
关于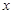 轴的对称点为
轴的对称点为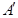 ,求证:直线
,求证:直线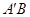 过定点.
过定点.
在平面直角坐标系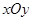 中,动点
中,动点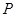 到两点
到两点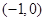 ,
,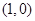 的距离之和等于
的距离之和等于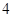 ,设点
,设点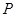 的轨迹为曲线
的轨迹为曲线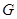 ,直线
,直线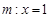 与曲线
与曲线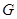 交于点
交于点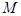 (点
(点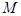 在第一象限).
在第一象限).
(Ⅰ)求曲线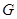 的方程;
的方程;
(Ⅱ)已知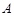 为曲线
为曲线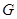 的左顶点,平行于
的左顶点,平行于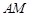 的直线
的直线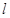 与曲线
与曲线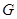 相交于
相交于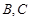 两点.判断直线
两点.判断直线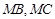 是否关于直线
是否关于直线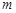 对称,并说明理由.
对称,并说明理由.
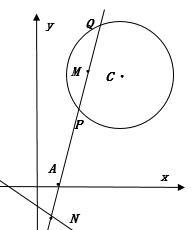
已知圆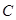 :
: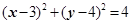 ,直线
,直线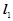 过定点
过定点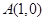 .
.
(1)若直线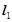 与圆相切,切点为
与圆相切,切点为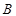 ,求线段
,求线段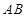 的长度;
的长度;
(2)若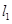 与圆相交于
与圆相交于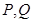 两点,线段
两点,线段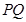 的中点为
的中点为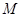 ,又
,又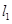 与
与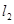 :
: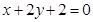 的交点为
的交点为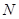 ,判断
,判断 •
•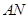 是否为定值,若是,则求出定值;若不是,请说明理由.
是否为定值,若是,则求出定值;若不是,请说明理由.
某工厂某种航空产品的年固定成本为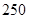 万元,每生产
万元,每生产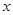 件,需另投入成本为
件,需另投入成本为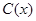 ,当年产量不足
,当年产量不足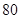 件时,
件时,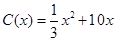 (万元).当年产量不小于
(万元).当年产量不小于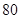 件时,
件时,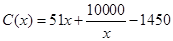 (万元).每件商品售价为
(万元).每件商品售价为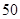 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润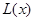 (万元)关于年产量
(万元)关于年产量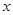 (件)的函数解析式;
(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?