以下命题正确的是: .
①把函数 的图象向右平移
的图象向右平移 个单位,可得到
个单位,可得到 的图象;
的图象;
②四边形 为长方形,
为长方形, 为
为 中点,在长方形
中点,在长方形 内随机取一点
内随机取一点 ,取得的
,取得的 点到
点到 的距离大于1的概率为
的距离大于1的概率为 ;
;
③等差数列 前
前 项和为
项和为 ,则三点
,则三点 ,
, ,
, 共线;
共线;
④已知 是定义在
是定义在 上的函数
上的函数 的导函数,且满足
的导函数,且满足 ,则不等式
,则不等式 的解集为
的解集为 .
.
已知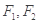 是双曲线
是双曲线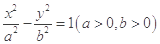 的左右两个焦点,过点
的左右两个焦点,过点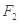 与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点
与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点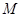 ,若点
,若点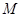 在以线段
在以线段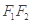 为直径的圆外,则该双曲线离心率的取值范围是( )
为直径的圆外,则该双曲线离心率的取值范围是( )
A.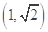 |
B. |
C.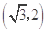 |
D.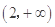 |
对任意的实数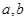 ,记
,记 ,若
,若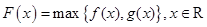 ,其中奇函数
,其中奇函数 在
在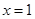 时有极小值-2,
时有极小值-2,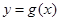 是正比例函数,函数
是正比例函数,函数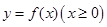 与函数
与函数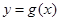 的图象如图所示.则下列关于函数
的图象如图所示.则下列关于函数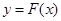 的说法中,正确的是( )
的说法中,正确的是( )
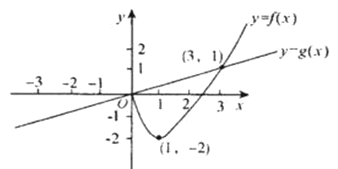
A.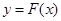 为奇函数 为奇函数 |
B.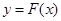 在 在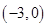 为增函数 为增函数 |
C.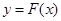 有极大值 有极大值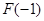 ,极小值 ,极小值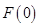 |
D.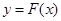 最小值为-2,最大值为2 最小值为-2,最大值为2 |
已知函数 其中
其中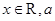 为参数.
为参数.
(1)记函数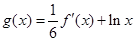 ,讨论函数
,讨论函数 的单调性;
的单调性;
(2)若曲线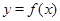 与
与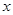 轴正半轴有交点且交点为
轴正半轴有交点且交点为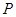 ,曲线在点
,曲线在点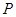 处的切线方程为
处的切线方程为 ,求证:对于任意的正实数
,求证:对于任意的正实数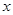 ,都有
,都有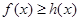 .
.
已知函数 R).
R).
(1)若曲线 在点
在点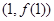 处的切线与直线
处的切线与直线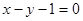 平行,求
平行,求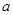 的值;
的值;
(2)在(1)条件下,求函数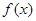 的单调区间和极值;
的单调区间和极值;
(3)当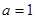 ,且
,且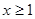 时,证明:
时,证明: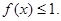
已知椭圆 的左顶点为
的左顶点为 ,
, 是椭圆
是椭圆 上异于点
上异于点 的任意一点,点
的任意一点,点 与点
与点 关于点
关于点 对称.
对称.
(1)若点 的坐标为
的坐标为 ,求
,求 的值;
的值;
(2)若椭圆 上存在点
上存在点 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
我们把离心率 的双曲线
的双曲线 称为黄金双曲线.如图是双曲线
称为黄金双曲线.如图是双曲线 的图象,给出以下几个说法:
的图象,给出以下几个说法:

①双曲线 是黄金双曲线;
是黄金双曲线;
②若 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;
③若 为左右焦点,
为左右焦点, 为左右顶点,
为左右顶点, 且
且 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;
④若 经过右焦点
经过右焦点 且
且 ,
, ,则该双曲线是黄金双曲线.
,则该双曲线是黄金双曲线.
其中正确命题的序号为 .
已知三棱锥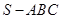 的底面是以
的底面是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,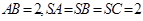 ,则三棱锥的外接球的球心到平面
,则三棱锥的外接球的球心到平面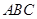 的距离是( )
的距离是( )
A.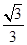 |
B.1 | C.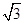 |
D.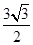 |
设等差数列{an}的公差为d,点(an,bn)在函数f (x)=2x的图象上(n∈N*).
(Ⅰ)证明:数列{bn}为等比数列;
(Ⅱ)若a1=1,直线y=(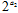 ln2)(x-a2)+
ln2)(x-a2)+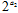 在x轴上的截距为2-
在x轴上的截距为2-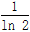 ,求数列{anb
,求数列{anb }的前n项和Sn.
}的前n项和Sn.