已知面 ,
, ,直线
,直线 ,直线
,直线 ,
, 斜交,则( )
斜交,则( )
A. 和 和 不垂直但可能平行 不垂直但可能平行 |
B. 和 和 可能垂直也可能平行 可能垂直也可能平行 |
C. 和 和 不平行但可能垂直 不平行但可能垂直 |
D. 和 和 既不垂直也不平行 既不垂直也不平行 |
下列说法正确的是_________(请把你认为正确说法的序号都填上).
①与 共线的单位向量是
共线的单位向量是 ;
;
②函数 的最小正周期为
的最小正周期为 ;
;
③ 是偶函数;
是偶函数;
④ 是
是 所在平面内一点,若
所在平面内一点,若 ,则
,则 是
是 的垂心;
的垂心;
⑤若函数 的值域为
的值域为 ,则
,则 的取值范围是
的取值范围是 .
.
定义在R上的函数f(x)满足f(x)-f(-x)=0,且对任意x,x∈[0,+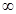 )(x1
)(x1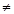 x2),都有
x2),都有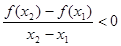 ,则( )
,则( )
| A.f(3)<f(-2)<f(1) |
| B.f(1)<f(-2)<f(3) |
| C.f(-2)<f(1)<f(3) |
| D.f(3)<f(1)<f(-2) |
已知函数 ,其中
,其中 为常数,且函数
为常数,且函数 图像过原点.
图像过原点.
(1)求 的值;
的值;
(2)证明:函数 在[0,2]上是单调递增函数;
在[0,2]上是单调递增函数;
(3)已知函数 ,求g(x)≥0时x的取值范围.
,求g(x)≥0时x的取值范围.
已知椭圆 的右焦点为
的右焦点为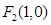 ,点
,点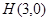 在椭圆上.
在椭圆上.
(1)求椭圆的方程;
(2)点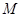 在圆
在圆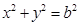 上,且
上,且 在第一象限,过
在第一象限,过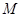 作圆
作圆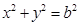 的切线交椭圆于
的切线交椭圆于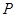 ,
,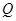 两点,求证:△
两点,求证:△ 的周长是定值.
的周长是定值.
设椭圆 的左右焦点分别为
的左右焦点分别为 ,焦距为
,焦距为 ,直线
,直线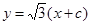 与椭圆的一个交点为
与椭圆的一个交点为 ,若
,若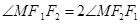 ,则椭圆离心率为( )
,则椭圆离心率为( )
A.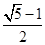 |
B.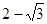 |
C.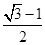 |
D.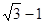 |