已知函数 ,且
(1) 试用含 的代数式表示b,并求 的单调区间;
(2)令 ,设函数 在 处取得极值,记点 , , , ,请仔细观察曲线 在点P处的切线与线段MP的位置变化趋势,并解释以下问题:
(Ⅰ)若对任意的 ,线段MP与曲线 均有异于M,P的公共点,试确定t的最小值,并证明你的结论;
(Ⅱ)若存在点 , ,使得线段 与曲线 有异于 、 的公共点,请直接写出 的取值范围(不必给出求解过程)
已知A,B 分别为曲线C: 与x轴的左、右两个交点,直线 过点B,且与 轴垂直,S为 上异于点B的一点,连结AS交曲线C于点T.
(1)若曲线C为半圆,点T为圆弧 的三等分点,试求出点S的坐标;
(2)如图,点M是以SB为直径的圆与线段TB的交点,试问:是否存在 ,使得O,M,S三点共线?若存在,求出 的值,若不存在,请说明理由。
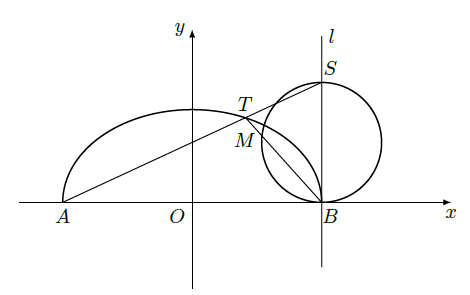
如图,某市拟在长为的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段 ,该曲线段为函数 , 的图象,且图象的最高点为 ;赛道的后一部分为折线段 ,为保证参赛运动员的安全,限定

(Ⅰ)求A , 的值和M,P两点间的距离;
(Ⅱ)应如何设计,才能使折线段赛道 最长?
如图,四边形 是边长为 的正方形, , ,且 , 为 的中点.
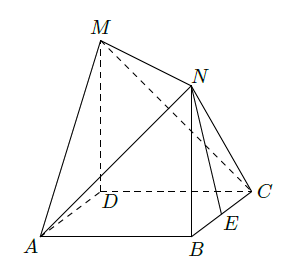
(1)求异面直线NE与AM所成角的余弦值
(2)在线段AN上是否存在点S,使得 ?若存在,求线段AS的长;若不存在,请说明理由
从集合 的所有非空子集中,等可能地取出一个。
(1)记性质r:集合中的所有元素之和为10,求所取出的非空子集满足性质r的概率;
(2)记所取出的非空子集的元素个数为 ,求 的分布列和数学期望
五位同学围成一圈依序循环报数,规定:
①第一位同学首次报出的数为1,第二位同学首次报出的数也为1,之后每位同学所报出的数都是前两位同学所报出的数之和;
②若报出的数为3的倍数,则报该数的同学需拍手一次
已知甲同学第一个报数,当五位同学依序循环报到第100个数时,甲同学拍手的总次数为________.
过抛物线 的焦点F作倾斜角为 的直线交抛物线于A、B两点,若线段AB的长为8,则 ________________.
某校开展"爱我海西、爱我家乡"摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示。记分员在去掉一个最高分和一个最低分后,算的平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清。若记分员计算无误,则数字 应该是___________

函数 的图象关于直线 对称。据此可推测,对任意的非零实数a,b,c,m,n,p,关于x的方程 的解集都不可能是( )
| A. |
B C D |
设a,b,c为同一平面内具有相同起点的任意三个非零向量,且满足a与b不共线, , ,则 的值一定等于 ( )
| A. |
以a,b为两边的三角形面积 |
B. |
以b,c为两边的三角形面积 |
| C. |
以a,b为邻边的平行四边形的面积 |
D. |
以b,c为邻边的平行四边形的面积 |
已知某运动员每次投篮命中的概率都为40%。现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果。经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
| A. |
0.35 B 0.25 C 0.20 D 0.15 |
设 是平面 内的两条不同直线, ,是平面 内的两条相交直线,则 的一个充分而不必要条件是( )
| A. |
且 |
B. |
且 |
| C. |
且 |
D. |
且 |