函数 在R上单调递减,且关于 的方程 恰好有两个不相等的实数解,则 a的取值范围是( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知△ ABC是边长为1的等边三角形,点 D、 E分别是边 AB 、 BC的中点,连接 DE并延长到点 F,使得 , 则 的值为( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知双曲线 ,以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于 A、 B、 C、 D四点,四边形的 ABCD的面积为2 b , 则双曲线的方程为( )
| A. |
|
B. |
|
C. |
|
D. |
|
设 是首项为正数的等比数列,公比为 , 则 是"对任意的正整数 , "的( )
| A. |
充要条件 |
B. |
充分而不必要条件 |
C. |
必要而不充分条件 |
D. |
既不充分也不必要条件 |
阅读右边的程序框图,运行相应的程序,则输出 S的值为( )
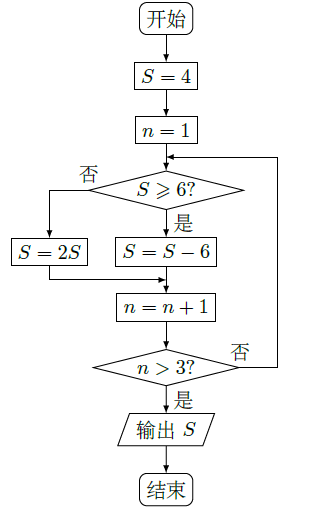
| A. | 2 |
B. | 4 |
C. | 6 |
D. | 8 |
设变量 , 满足约束条件 ,则目标函数 的最小值为( )
| A. |
|
B. |
6 |
C. |
10 |
D. |
17 |
设 ,且曲线 在 处的切线与x轴平行。
(Ⅰ)求 的值,并讨论 的单调性;
(Ⅱ)证明:当
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:

(Ⅰ)试分别估计两个分厂生产的零件的优质品率;
(Ⅱ)由于以上统计数据填下面 列联表,并问是否有99%的把握认为"两个分厂生产的零件的质量有差异"。
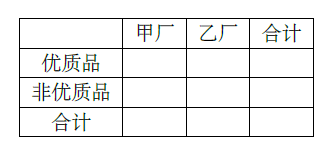
附:
如图,已知两个正方形ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点。

(Ⅰ)若 , ,求直线MN的长;
(Ⅱ)用反证法证明:直线ME与BN是两条异面直线。
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为 , ,于水面C处测得B点和D点的仰角均为 ,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km, 1.414, 2.449)

等比数列 的前n 项和为 ,已知 , , 成等差数列
(1)求 的公比 ;
(2)求
求

