如图,在 中, ,点 在 上, ,点 在 上,连接 , ,作 ,垂足为 .
(1)如图 ,当 时,连接 ,过点 作 交 的延长线于点 .
①求证: ;
②请猜想三条线段 , , 之间的数量关系,直接写出结论;
(2)如图 ,当 时,三条线段 , , 之间存在怎样的数量关系?请证明你的结论.

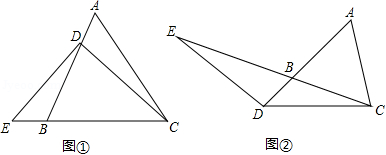
(1)已知: 是等腰三角形,其底边是 ,点 在线段 上, 是直线 上一点,且 ,若 (如图①).求证: ;
(2)若将(1)中的“点 在线段 上”改为“点 在线段 的延长线上”,其它条件不变(如图②),(1)的结论是否成立,并说明理由;
(3)若将(1)中的“若 ”改为“若 ”,其它条件不变,则 的值是多少?(直接写出结论,不要求写解答过程)
中, , ,过点 作直线 ,使 ,点 在直线 上,作射线 ,将射线 绕点 顺时针旋转角 后交直线 于点 .
(1)如图①,当 ,且点 在射线 上时,直接写出线段 , , 的数量关系.
(2)如图②,当 ,且点 在射线 上时,直写出线段 、 、 的数量关系,并说明理由.
(3)当 时,若点 在射线 上, , ,请直接写出线段 的长度.

如图, 中, , 垂直平分 ,交线段 于点 (点 与点 不重合),点 为 上一点,点 为 上一点(点 与点 不重合),且 .
(1)如图1,当 时,线段 和 的数量关系是 .
(2)如图2,当 时,猜想线段 和 的数量关系,并加以证明.
(3)若 , , ,请直接写出 的长.

我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在 中, 是 边上的中线, 与 的“极化值”就等于 的值,可记为 △ .
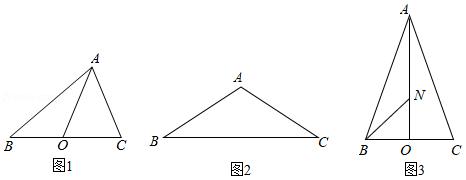
(1)在图1中,若 , , , 是 边上的中线,则 △ , △ ;
(2)如图2,在 中, , ,求 △ 、 △ 的值;
(3)如图3,在 中, , 是 边上的中线,点 在 上,且 .已知 △ , △ ,求 的面积.
如图,在四边形 中, , , 、 分别是 、 的中点,连接 、 、 .若四边形 的面积为6,则 的面积为

A.2B. C. D.3
已知,在 中, , 是 边上一点,连接 ,分别以 和 为直角边作 和 ,使 ,点 , 在 下方,连接 .
(1)如图1,当 , , 时,
求证:① ,② ;
(2)如图2,当 , , 时,猜想 和 之间的数量关系?并说明理由.
如图, 是等腰直角三角形, , 是射线 上一点(点 不与点 重合),以 为斜边作等腰直角三角形 (点 和点 在 的同侧),连接 .
(1)如图①,当点 与点 重合时,直接写出 与 的位置关系;
(2)如图②,当点 与点 不重合时,(1)的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
(3)当 时,请直接写出 的值.

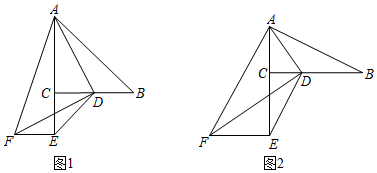
如图,是具有公共边 的两个直角三角形,其中, , .
(1)如图1,若延长 到点 ,使 ,连接 , .
①求证: , ;
②求证: ;
(2)若 与 位置如图2所示,请直接写出线段 , , 的数量关系.

已知:在 外分别以 , 为边作 与 .
(1)如图1, 与 分别是以 , 为斜边的等腰直角三角形,连接 .以 为直角边构造 ,且 ,连接 , , .
求证:① .
②四边形 是平行四边形.
(2)小明受到图1的启发做了进一步探究:
如图2,在 外分别以 , 为斜边作 与 ,并使 ,取 的中点 ,连接 , 后发现,两者间存在一定的数量关系且夹角度数一定,请你帮助小明求出 的值及 的度数.
(3)小颖受到启发也做了探究:
如图3,在 外分别以 , 为底边作等腰三角形 和等腰三角形 ,并使 ,取 的中点 ,连接 , 后发现,当给定 时,两者间也存在一定的数量关系且夹角度数一定,若 , ,请你帮助小颖用含 , 的代数式直接写出 的值,并用含 的代数式直接表示 的度数.

已知:在 中, ,点 是 边上一点,连接 ,点 是线段 延长线上一点,连接 , ,使 ,过点 作 ,交 于点 .
(1)①如图1,当 时,线段 与 之间的数量关系是 .
②如图2,当 时,线段 与 之间的数量关系是 .
(2)如图3,当 时,线段 与 之间具有怎样的数量关系?请说明理由.
(3)如图4,当 时,直接写出线段 与 之间的数量关系.(用含 的式子表示)

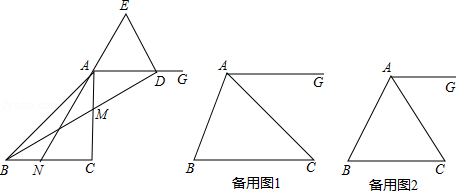
已知: 是等腰三角形, , .点 在边 上,点 在边 上(点 、点 不与所在线段端点重合), ,连接 , ,射线 ,延长 交射线 于点 ,点 在直线 上,且 .
(1)如图,当 时
①求证: ;
②求 的度数;
(2)当 ,其它条件不变时, 的度数是 ;(用含 的代数式表示)
(3)若 是等边三角形, ,点 是 边上的三等分点,直线 与直线 交于点 ,请直接写出线段 的长.
在 中, ,点 是 的中点,点 是 上的一个动点(点 不与点 , , 重合).过点 ,点 作直线 的垂线,垂足分别为点 和点 ,连接 , .
(1)如图1,请直接写出线段 与 的数量关系;
(2)如图2,当 时,请判断线段 与 之间的数量关系和位置关系,并说明理由
(3)若 , ,当 为等腰三角形时,请直接写出线段 的长.

如图,在 中, , , 于点 .
(1)如图1,点 , 在 , 上,且 .求证: ;
(2)点 , 分别在直线 , 上,且 .
①如图2,当点 在 的延长线上时,求证: ;
②当点 在点 , 之间,且 时,已知 ,直接写出线段 的长.
