中, , ,过点 作直线 ,使 ,点 在直线 上,作射线 ,将射线 绕点 顺时针旋转角 后交直线 于点 .
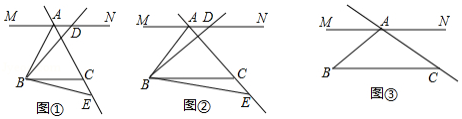
(1)如图①,当 ,且点 在射线 上时,直接写出线段 , , 的数量关系.
(2)如图②,当 ,且点 在射线 上时,直写出线段 、 、 的数量关系,并说明理由.
(3)当 时,若点 在射线 上, , ,请直接写出线段 的长度.
相关知识点
推荐套卷
中, , ,过点 作直线 ,使 ,点 在直线 上,作射线 ,将射线 绕点 顺时针旋转角 后交直线 于点 .
(1)如图①,当 ,且点 在射线 上时,直接写出线段 , , 的数量关系.
(2)如图②,当 ,且点 在射线 上时,直写出线段 、 、 的数量关系,并说明理由.
(3)当 时,若点 在射线 上, , ,请直接写出线段 的长度.
