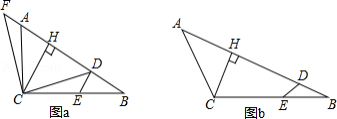
如图,在 中, ,点 在 上, ,点 在 上,连接 , ,作 ,垂足为 .
(1)如图 ,当 时,连接 ,过点 作 交 的延长线于点 .
①求证: ;
②请猜想三条线段 , , 之间的数量关系,直接写出结论;
(2)如图 ,当 时,三条线段 , , 之间存在怎样的数量关系?请证明你的结论.
相关知识点
推荐套卷
如图,在 中, ,点 在 上, ,点 在 上,连接 , ,作 ,垂足为 .
(1)如图 ,当 时,连接 ,过点 作 交 的延长线于点 .
①求证: ;
②请猜想三条线段 , , 之间的数量关系,直接写出结论;
(2)如图 ,当 时,三条线段 , , 之间存在怎样的数量关系?请证明你的结论.
