下列叙述错误的是( ).
A.若事件 发生的概率为 发生的概率为 ,则 ,则 |
| B.互斥事件不一定是对立事件,但是对立事件一定是互斥事件 |
| C.5张奖券中有一张有奖,甲先抽,乙后抽,则乙与甲中奖的可能性相同 |
| D.某事件发生的概率是随着试验次数的变化而变化的 |
某入伍新兵在打靶训练中,连续射击2次,则事件“至少有1次中靶”的互斥事件是( )
| A.至多有一次中靶 | B.2次都中靶 |
| C.2次都不中靶 | D.只有一次中靶 |
下列说法一定正确的是( )
| A.一名篮球运动员,号称“百发百中”,若罚球三次,不会出现三投都不中的情况 |
B.一枚硬币掷一次得到正面的概率是 ,那么掷两次一定会出现一次正面的情况 ,那么掷两次一定会出现一次正面的情况 |
| C.如买彩票中奖的概率是万分之一,则买一万元的彩票一定会中奖一元 |
| D.随机事件发生的概率与试验次数无关 |
下列四个命题:
①对立事件一定是互斥事件
②若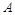 、
、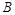 为两个事件,则
为两个事件,则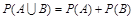
③若事件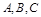 两两互斥,则
两两互斥,则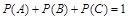
④若事件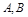 满足
满足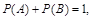 则
则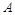 、
、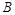 是对立事件.
是对立事件.
其中错误命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
从12个同类产品(其中有10个正品,2个次品)中任意抽取3个,下列事件是必然事件的是
| A.3个都是正品 | B.至少有一个是次品 |
| C.3个都是次品 | D.至少有一个是正品 |
(本小题满分10分)
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑
球.现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为黑球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列,并求其数学期望E(
的分布列,并求其数学期望E( ).
).
袋子中装有编号为 ,
, ,
, 的3个黑球和编号为
的3个黑球和编号为 ,
, 的2个红球,从中任意摸出2个球.
的2个红球,从中任意摸出2个球.
(Ⅰ)写出所有不同的结果;
(Ⅱ)求恰好摸出1个黑球和1个红球的概率;
(Ⅲ)求至少摸出1个红球的概率.
一个篮球运动员投篮一次得 分的概率为
分的概率为 ,得
,得 分的概率为
分的概率为 ,得
,得 分的概率为
分的概率为 (投篮一次得分只能
(投篮一次得分只能 分、
分、 分、
分、 分或
分或 分),其中
分),其中 ,已知他投篮一次得分的数学期望为
,已知他投篮一次得分的数学期望为 ,则
,则 的最大值为( )
的最大值为( )
A. |
B. |
C. |
D. |
马老师从课本上抄录一个随机变量 的概率分布律如下表
的概率分布律如下表
请小牛同学计算 的数学期望,尽管“!”处无法完全看清,且两个“?”处字迹模糊,但能肯定这两个“?”处的数值相同。据此,小牛给出了正确答案
的数学期望,尽管“!”处无法完全看清,且两个“?”处字迹模糊,但能肯定这两个“?”处的数值相同。据此,小牛给出了正确答案
某班在联欢会上举行一个抽奖活动,甲箱中有3个红球,2个黑球,乙箱中装有2个红球4个黑球,参加活动者从这两个箱子中分别摸出1个球,如果摸到的都是红球则获奖.
(Ⅰ)求每个活动参加者获奖的概率;
(Ⅱ)某办公室共有5人,每人抽奖1次,求这5人中至少有3人获奖的概率.
从装有3个红球,3个白球的袋中随机取出2个球,设其中有 个红球,则
个红球,则 =
=
在20件产品中,有15件一级品,5件二级品,从中任取3件,其中至少有
一件为二级品的概率是: (用数字作答)。
下列叙述随机事件的频率与概率的关系中哪个是正确的( )
| A.频率就是概率 |
| B.频率是客观存在的,与试验次数无关 |
| C.概率是随机的,在试验前不能确定 |
| D.随着试验次数的增加,频率一般会越来越接近概率 |