(本小题满分12分)
某家电生产企业市场营销部对本厂生产的某种电器进行了市场调查,发现每台的销售利润与该电器的无故障使用时间 (单位:年)有关.若
(单位:年)有关.若 ,则销售利润为
,则销售利润为 元;若
元;若 ,则销售利润为
,则销售利润为 元;若
元;若 ,则销售利润为
,则销售利润为 元,设每台该种电器的无故障使用时间
元,设每台该种电器的无故障使用时间 ,
, ,
, 这三种情况发生的概率分别是
这三种情况发生的概率分别是 ,又知
,又知 是方程
是方程 的两个根,且
的两个根,且 .
.
(1)求 的值;
的值;
(2)记 表示销售两台该种电器的销售利润总和,求
表示销售两台该种电器的销售利润总和,求 的分布列及期望.
的分布列及期望.
现有10个数,它们能构成一个以1为首项,-3为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是______.
如图所示,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,则它的涂漆面数为2的概率( )
A. |
B. |
C. |
D. |
如图,长方体ABCD—A1B1C1D1,有一动点在此长方体内随机运动,则此动点在三棱锥A—A1BD内的概率为 .
有驱虫药1618和1573各3杯,从中随机取出3杯称为一次试验(假定每杯被取到的概率相等),将1618全部取出称为试验成功.
(1)求一次试验成功的概率.
(2)求恰好在第3次试验成功的概率(要求将结果化为最简分数).
某城市要建成宜商、宜居的国际化现代新城,该城市的东城区、西城区分别引进8甲厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
(1)根据茎叶图判断哪个区域厂家的平均分较高;
(2)规定85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5分的概率.
在30瓶饮料中,有3瓶已过了保质期,从这30瓶饮料中任取2瓶,则至少取到1瓶已过保质期的概率为________(结果用最简分数表示).
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在一次游戏中,①摸出3个白球的概率,②获奖的概率;
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X).
本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租不超过两小时免费,超过两小时的收费标准为2元(不足1小时的部分按1小时计算).有人独立来该租车点则车骑游.各租一车一次.设甲、乙不超过两小时还车的概率分别为 ,
, ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为 ,
, ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(1)求出甲、乙所付租车费用相同的概率;
(2)求甲、乙两人所付的租车费用之和为随机变量X,求X的分布列与数学期望E(X).
容量为20的样本数据,分组后的频数如下表:
则样本数据落在区间[10,40)的频率为( )
| A.0.35 | B.0.45 | C.0.55 | D.0.65 |
某种动物由出生算起活到20岁的概率为0.8,活到25岁的概率为0.4,现有一个20岁的动物,求它能活到25岁的概率.
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量的线性相关性越强,相关系数的绝对值越接近于1;
③在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0),若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8 ;
④对分类变量X与Y的随机变量k2的观测值k来说,k越小,判断“X与Y有关系”的把握程度越大.
其中真命题的个数为( )
| A.4 | B.3 | C.2 | D.1 |
2013年12月21日上午10时,省会首次启动重污染天气Ⅱ级应急响应,正式实施机车尾号限行,当天某报社为了解公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(1)完成被调查人员的频率分布直方图;
(2)若从年龄在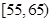 ,
,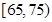 的被调查者中各随机选取1人进行追踪调查,求两人中至少有1人赞成“车辆限行”的概率.
的被调查者中各随机选取1人进行追踪调查,求两人中至少有1人赞成“车辆限行”的概率. 
(本小题满分12分)为迎接2014年“马”年的到来,某校举办猜奖活动,参与者需先后回答两道选择题,问题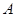 有三个选项,问题
有三个选项,问题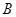 有四个选项,但都只有一个选项是正确的,正确回答问题
有四个选项,但都只有一个选项是正确的,正确回答问题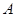 可获奖金
可获奖金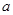 元,正确回答问题
元,正确回答问题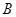 可获奖金
可获奖金 元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
(1)如果参与者先回答问题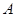 ,求其恰好获得奖金
,求其恰好获得奖金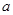 元的概率;
元的概率;
(2)试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.