某校有教职工 人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
(Ⅰ)随机抽取一人,是35岁以下的概率为 ,求
,求 的值;
的值;
(Ⅱ)从50岁以上的6人中随机抽取两人,求恰好只有一位是研究生的概率.
一个游戏转盘上有四种颜色:红、黄、蓝、黑,并且它们所占面积的比为6∶2∶1∶4,则指针停在红色或蓝色的区域的概率为 ( )
A.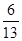 ; ; |
B. ; ; |
C. ; ; |
D.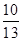 . . |
某高校从今年参加自主招生考试的学生中随机抽取容量为 的学生成绩样本,得到频率分布表如下:
的学生成绩样本,得到频率分布表如下:
| 组数 |
分组 |
频数 |
频率 |
| 第一组 |
[230,235) |
8 |
0.16 |
| 第二组 |
[235,240) |
 |
0.24 |
| 第三组 |
[240,245) |
15 |
 |
| 第四组 |
[245,250) |
10 |
0.20 |
| 第五组 |
[250,255] |
5 |
0.10 |
| 合计 |
 |
1.00 |
(1)求 的值;
的值;
(2)为了选拔出更加优秀的学生,该高校决定在第三、四、五组中用分层抽样的方法抽取6名学生进行第二轮考核,分别求第三、四、五组参加考核的人数;
(3)在(2)的前提下,高校决定从这6名学生中择优录取2名学生,求2人中至少有1人是第四组的概率.
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4。
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求

 +2的概率。
+2的概率。
已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如下表:
 |
A |
B |
C |
| A |
7 |
20 |
5 |
| B |
9 |
18 |
6 |
| C |
a |
4 |
b |
若抽取学生n人,成绩分为A(优秀)、B(良好)、C(及格)三个等级,设x,y分别表示数学成绩与地理成绩,例如:表中数学成绩为B等级的共有20+18+4=42人,已知x与y均为B等级的概率是0.18.
(1)若在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩为C等级的学生中,已知a≥10,b≥8,求数学成绩为A等级的人数比C等级的人数少的概率.
从1,2,3,4这四个数字中依次取(不放回)两个数 ,使得
,使得 的概率是( )
的概率是( )
A. |
B. |
C. |
D. |
在一个盒子里装有4枝圆珠笔,其中3枝一等品,1枝三等品
(1)从盒子里任取2枝恰有1枝三等品的概率多大?
(2)从盒子里第一次任取1枝(不放回),第二次任取1枝;第一次取的是三等品,第二次取的是一等品的概率有多大?
高三某班有两个数学课外兴趣小组,第一组有 名男生,
名男生, 名女生,第二组有
名女生,第二组有 名男生,
名男生, 名女生.现在班主任老师要从第一组选出
名女生.现在班主任老师要从第一组选出 人,从第二组选出
人,从第二组选出 人,请他们在班会上和全班同学分享学习心得.
人,请他们在班会上和全班同学分享学习心得.
(Ⅰ)求选出的 人均是男生的概率;
人均是男生的概率;
(Ⅱ)求选出的 人中有男生也有女生的概率.
人中有男生也有女生的概率.
一个袋中装有10个大小相同的小球.其中白球5个、黑球4个、红球1个.
(1)从袋中任意摸出2个球,求至少得到1个白球的概率;
(2)从袋中任意摸出3个球,记得到白球的个数为 ,求随机变量
,求随机变量 的数学期望
的数学期望 .
.
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取的20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到频率分布表如下:

(1)求表中 的值及分数在
的值及分数在 范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在
范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在 范围为及格);
范围为及格);
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.
(Ⅰ)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率;
(Ⅱ)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率.
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求 的概率.
的概率.
口袋内装有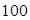 个大小相同的红球、白球和黑球,其中有
个大小相同的红球、白球和黑球,其中有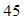 个红球,从中摸出
个红球,从中摸出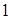 个球,若摸出白球的概率为
个球,若摸出白球的概率为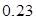 ,则摸出黑球的概率为____________.
,则摸出黑球的概率为____________.