[天津]2014届天津市高三第一次六校联考理科数学试卷
设 为向量,则“
为向量,则“ ”是“
”是“ ”的 ( )
”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
来源:2014届天津市高三第一次六校联考理科数学试卷
设双曲线 的半焦距为
的半焦距为 ,直线
,直线 过
过 两点,若原点
两点,若原点 到
到 的距离为
的距离为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. 或2 或2 |
B.2 | C. 或 或 |
D. |
来源:2014届天津市高三第一次六校联考理科数学试卷
某工厂生产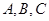 三种不同型号的产品,产品数量之比依次为
三种不同型号的产品,产品数量之比依次为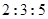 ,现用分层抽样方法抽出一个容量为
,现用分层抽样方法抽出一个容量为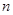 的样本,样本中
的样本,样本中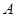 种型号产品有16件,那么此样本的容量
种型号产品有16件,那么此样本的容量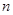 =
=
来源:2014届天津市高三第一次六校联考理科数学试卷
一个袋中装有10个大小相同的小球.其中白球5个、黑球4个、红球1个.
(1)从袋中任意摸出2个球,求至少得到1个白球的概率;
(2)从袋中任意摸出3个球,记得到白球的个数为 ,求随机变量
,求随机变量 的数学期望
的数学期望 .
.
来源:2014届天津市高三第一次六校联考理科数学试卷
如图,在四棱锥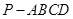 中,
中,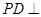 底面
底面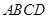 ,底面
,底面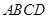 为正方形,
为正方形,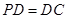 ,
,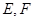 分别是
分别是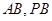 的中点.
的中点.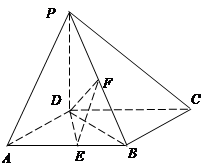
(1)求证: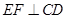 ;
;
(2)在平面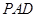 内求一点
内求一点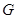 ,使
,使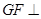 平面
平面 ,并证明你的结论;
,并证明你的结论;
(3)求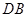 与平面
与平面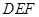 所成角的正弦值.
所成角的正弦值.
来源:2014届天津市高三第一次六校联考理科数学试卷
在直角坐标系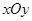 中,点
中,点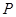 到两点
到两点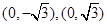 的距离之和等于4,设点
的距离之和等于4,设点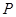 的轨迹为
的轨迹为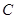 ,直线
,直线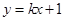 与
与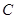 交于
交于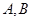 两点.
两点.
(1)写出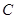 的方程;
的方程;
(2)若点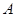 在第一象限,证明当
在第一象限,证明当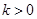 时,恒有
时,恒有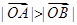 .
.
来源:2014届天津市高三第一次六校联考理科数学试卷
已知正项数列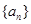 的前
的前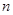 项和为
项和为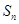 ,
,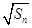 是
是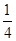 与
与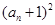 的等比中项.
的等比中项.
(1)求证:数列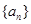 是等差数列;
是等差数列;
(2)若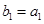 ,且
,且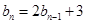 ,求数列
,求数列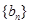 的通项公式;
的通项公式;
(3)在(2)的条件下,若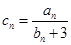 ,求数列
,求数列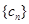 的前
的前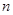 项和
项和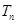 .
.
来源:2014届天津市高三第一次六校联考理科数学试卷
 为虚数单位,则
为虚数单位,则 = ( ).
= ( ).
 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值为( )
的最大值为( )
 ,则输出的数等于( )
,则输出的数等于( )









 中,
中, ,
, ,
, ,则
,则



 是定义在数集
是定义在数集 上的奇函数,且当
上的奇函数,且当 时,
时, 成立,若
成立,若 ,
, ,
, ,则
,则 的大小关系是( )
的大小关系是( )



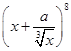 的展开式中
的展开式中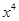 的系数为7,则实数
的系数为7,则实数 _________.
_________. 中,
中, ,
, ,则
,则 ________.
________. (
( )被曲线
)被曲线 所截的弦长 .
所截的弦长 . 经过圆心
经过圆心 ,
, ,
, 绕点
绕点 ,连
,连 交圆
交圆 ,则
,则 =________.
=________.
 不在直线
不在直线 的下方,则
的下方,则 的最小值为________.
的最小值为________.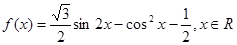
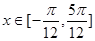 时,求函数
时,求函数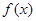 的最小值和最大值
的最小值和最大值 的对边分别为
的对边分别为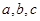 且
且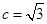 ,
,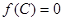 ,若
,若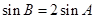 ,求
,求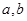 的值.
的值.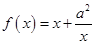 ,
,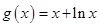 ,其中
,其中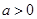 .
.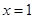 是函数
是函数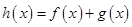 的极值点,求实数
的极值点,求实数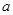 的值;
的值; (
(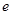 为自然对数的底数)都有
为自然对数的底数)都有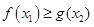 成立,求实数
成立,求实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号