2012年全国统一高考数学试卷(江苏卷)
某学校高一、高二、高三年级的学生人数之比为 ,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取名学生.
现有10个数,它们能构成一个以1为首项, 为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是.
为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是.
在平面直角坐标系 中,圆 的方程为 ,若直线 上至少存在一点,使得以该点为圆心,1为半径的圆与圆 有公共点,则 的最大值是.
如图,在直三棱柱 中, , 分别是棱 上的点(点 不同于点 ),且 为 的中点.

求证:(1)平面 平面
平面 ;
;
(2)直线
平面
.
如图,建立平面直角坐标系
,
轴在地平面上,
轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程
表示的曲线上,其中 与发射方向有关.炮的射程是指炮弹落地点的横坐标.
与发射方向有关.炮的射程是指炮弹落地点的横坐标.
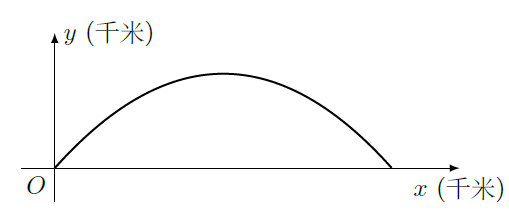
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标
不超过多少时,炮弹可以击中它?请说明理由.
若函数
在
处取得极大值或极小值,则称
为函数
的极值点.已知
是实数,1和-1是函数
的两个极值点.
(1)求
和
的值;
(2)设函数
的导函数
,求
的极值点;
(3)设
,其中
,求函数
的零点个数.
如图,在平面直角坐标系 中,椭圆 的左、右焦点分别为 .已知 和 都在椭圆上,其中 为椭圆的离心率.

(1)求椭圆的方程;
(2)设
是椭圆上位于
轴上方的两点,且直线
与直线
平行,
与
交于点
.
(i)若
,求直线
的斜率;
(ii)求证:
是定值.
已知各项均为正数的两个数列
和
满足:
,
(1)设
,求证:数列
是等差数列;
(2)设
,且
是等比数列,求
和
的值.
设
为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,
;当两条棱平行时,
的值为两条棱之间的距离;当两条棱异面时,
.
(1)求概率
;
(2)求
的分布列,并求其数学期望




 粤公网安备 44130202000953号
粤公网安备 44130202000953号