市民李生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机的.同一条道路去程与回程是否堵车互不影响.假设李生早上需要先开车送小孩去丙地小学,再返回经甲地赶去乙地上班,
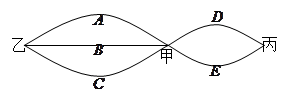
(1)写出李生可能走的所有路线;(比如DDA表示走D路从甲到丙,再走D路回到甲,然后走A路到达乙);
(2)假设从丙地到甲地时若选择走道路D会遇到拥堵,并且从甲地到乙地时若选择走道路B也会遇到拥堵,其它方向均通畅,但李生不知道相关信息,那么从出发到回到上班地没有遇到过拥堵的概率是多少?