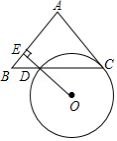
如图,在 中, ,点 是 边长一点, ,垂足为点 ,点 在线段 的延长线上,且 经过 , 两点.
(1)判断直线 与 的位置关系,并说明理由;
(2)若 的半径为2, 的长为 ,请求出 的度数.
随机抽取某小吃店一周的营业额(单位:元)如下表:
|
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
星期日 |
合计 |
|
540 |
680 |
640 |
640 |
780 |
1110 |
1070 |
5460 |
(1)分析数据,填空:这组数据的平均数是 元,中位数是 元,众数是 元.
(2)估计一个月的营业额(按30天计算)
①星期一到星期五营业额相差不大,用这5天的平均数估算合适么?
答(填“合适”或“不合适” .
②选择一个你认为最合适的数据估算这个小吃店一个月的营业额.
新冠疫情期间,口罩成为了人们出行必备的防护工具.某药店三月份共销售 , 两种型号的口罩9000只,共获利润5000元,其中 , 两种型号口罩所获利润之比为 .已知每只 型口罩的销售利润是 型口罩的1.2倍.
(1)求每只 型口罩和 型口罩的销售利润;
(2)该药店四月份计划一次性购进两种型号的口罩共10000只,其中 型口罩的进货量不超过 型口罩的1.5倍,设购进 型口罩 只,这10000只口罩的销售总利润为 元.该药店如何进货,才能使销售总利润最大?
某数学小组开展测量物体高度的实践活动,他们要测量某建筑物上悬挂的电子显示屏的高度.如图所示,他们先在点 测得电子显示屏底端点 的仰角 ,然后向建筑物的方向前进 到达点 ,又测得电子显示屏顶端点 的仰角 ,测得电子显示屏底端点 的仰角 .(点 , , 在同一条直线上,且与点 , 在同一平面内,不考虑测角仪高度)
(1)求此时他们离建筑的距离 的长;
(2)求电子显示屏 的高度.
(以上结果用含根号的式子表示)

为提高中小学生的身体素质,各校大力开展校园足球活动,某体育用品商店抓住这一商机,第一次用30000元购进 , 两种型号的足球,并很快销售完毕,共获利12200元,其进价和售价如下表:
|
|
|
|
|
进价(元 个) |
120 |
200 |
|
售价(元 个) |
170 |
280 |
(1)该体育用品商店购进 , 两种型号的足球各多少个?
(2)该体育用品商店第二次准备用不超过40000元的资金再次购进 , 两种型号的足球共260个,最少购进 种型号的足球多少个?
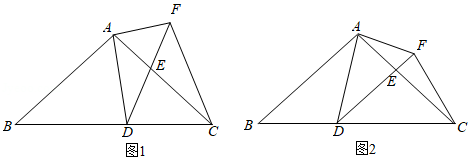
如图1,在 中, , ,点 为 边上的动点(点 不与点 , 重合).以 为顶点作 ,射线 交 边于点 ,过点 作 交射线 于点 ,连接 .
(1)求证: ;
(2)当 时(如图 ,求 的长;
(3)点 在 边上运动的过程中,是否存在某个位置,使得 ?若存在,求出此时 的长;若不存在,请说明理由.
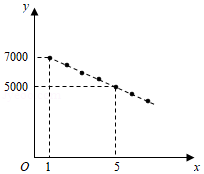
随着 技术的发展,人们对各类 产品的使用充满期待,某公司计划在某地区销售一款 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第 为正整数)个销售周期每台的销售价格为 元, 与 之间满足如图所示的一次函数关系.
(1)求 与 之间的关系式;
(2)设该产品在第 个销售周期的销售数量为 (万台), 与 的关系可以用 来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
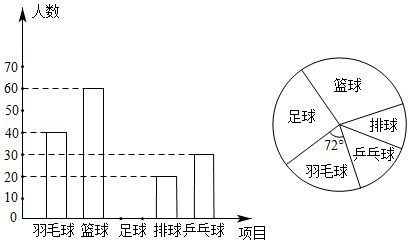
奥体中心为满足暑期学生对运动的需求,欲开设球类课程,该中心随机抽取部分学生进行问卷调查,被调查学生须从“羽毛球”、“篮球”、“足球”、“排球”、“乒乓球”中选择自己最喜欢的一项.根据调查结果绘制了不完整的条形统计图和扇形统计图,请根据图中信息,解答下列问题:
(1)此次共调查了多少名学生?
(2)将条形统计图补充完整;
(3)我们把“羽毛球”“篮球”,“足球”、“排球”、“乒乓球”分别用 , , , , 表示.小明和小亮分别从这些项目中任选一项进行训练,利用树状图或表格求出他俩选择不同项目的概率.
为进一步发展学生特长,某校要开设编织、摄影、航模、机器人四门校本课程,规定每名学生必须且只能选修一门校本课程,学校对学生选修本课程的情况进行了抽样调查,根据调查结果绘制了下面两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题.
(1)本次调查,一共调查了 名学生;
(2)补全条形统计图和扇形统计图;
(3)若该学校共有1700名学生据此估计有多少名学生选修航模;
(4)将2名选修摄影的学生和2名选修编织的学生编为一组,从中随机抽取2人,请用列表或画树状图的方法求出2人都选修编织的概率.
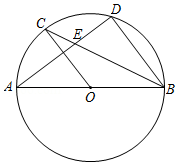
如图, 为 的直径, , 为圆上的两点, ,弦 , 相交于点 .
(1)求证: ;
(2)若 , ,求 的半径;
(3)在(2)的条件下,过点 作 的切线,交 的延长线于点 ,过点 作 交 于 , 两点(点 在线段 上),求 的长.
如图,在平面直角坐标系 中,一次函数 和 的图象相交于点 ,反比例函数 的图象经过点 .
(1)求反比例函数的表达式;
(2)设一次函数 的图象与反比例函数 的图象的另一个交点为 ,连接 ,求 的面积.
