新冠疫情期间,口罩成为了人们出行必备的防护工具.某药店三月份共销售 , 两种型号的口罩9000只,共获利润5000元,其中 , 两种型号口罩所获利润之比为 .已知每只 型口罩的销售利润是 型口罩的1.2倍.
(1)求每只 型口罩和 型口罩的销售利润;
(2)该药店四月份计划一次性购进两种型号的口罩共10000只,其中 型口罩的进货量不超过 型口罩的1.5倍,设购进 型口罩 只,这10000只口罩的销售总利润为 元.该药店如何进货,才能使销售总利润最大?
相关知识点
推荐套卷
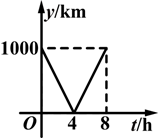
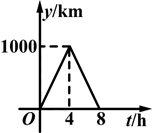
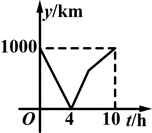
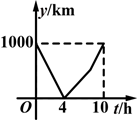
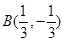 是否在此函数的图象上;
是否在此函数的图象上;

 粤公网安备 44130202000953号
粤公网安备 44130202000953号