初中数学解答题

把下列各数分别填入相应的集合里．
－1．8，0，，0．1，－，－1．4343343334…（每两个4之间1的个数逐次加1），．
正数集合：（     …）；
负数集合：（     …）；
有理数集合：（    …）；
无理数集合：（    …）．

如图，长方形ABCO的顶点A、C、O都在坐标轴上，点B的坐标为（8，3），M为AB的中点．

（1）试求点M的坐标和△AOM的周长；
（2）若P是OC上的一个动点，它以每秒1个单位长度的速度从点C出发沿射线CO方向匀速运动，设运动时间为t秒（t＞0）．
①若△POM的面积等于△AOM的面积的一半，试求t的值；
②是否存在某一时刻t，使△POM是等腰三角形？若存在，求出此时t的值；若不存在，试说明理由．

如图，点N是△ABC的边BC延长线上的一点，∠ACN=2∠BAC， 过点A作AC的垂线交CN于点P．

（1）若∠APC=30°，求证：AB=AP；
（2）若AP=8，BP=16，求AC的长；
（3）若点P在BC的延长线上运动，∠APB的平分线交AB于点M．你认为∠AMP的大小是否发生变化？若变化，请说明理由；若不变化，求出∠AMP的大小．

如图，在△ABC中，CE⊥BA的延长线于E，BF⊥CA的延长线于F，M为BC的中点，分别连接ME、MF、EF．
  
（1）若EF＝3，BC＝8，求△EFM的周长；
（2）若∠ABC＝28°，∠ACB＝48°，求△EFM的三个内角的度数．

勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：
将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，
求证：a²+b²=c²
证明：连结DB，过点D作BC边上的高DF，则DF=EC=b﹣a．
∵S_{四边形ADCB}=S_△ACD+S_△ABC=b²+ab．
又∵S_{四边形ADCB}=S_△ADB+S_△DCB=c²+a（b﹣a）．
∴b²+ab=c²+a（b﹣a），  ∴a²+b²=c²．

请参照上述证法，利用图2完成下面的证明．
将两个全等的直角三角形按图2所示摆放，其中∠ABC=90°．
求证：a²+b²=c²．
证明：

如图，在8×8网格纸中，每个小正方形的边长都为1．

（1）请在网格纸中建立平面直角坐标系，使点A、C的坐标分别为（－4，4），（－1，3），并写出点B的坐标为      ；
（2）画出△ABC关于y轴的对称图形△A₁B₁C₁，并写出B₁点的坐标；
（3）在y轴上求作一点P，使△PAB的周长最小，并直接写出点P的坐标．

按下列要求确定点的坐标．

（1）已知点A在第四象限，且到x轴距离为1，到y轴距离为5，求点A的坐标；
（2）已知点B（a－1，－2a+8），且点B在第一、三象限的角平分线上，求a；
（3）试判断（1）、（2）中的点A、B与坐标原点O围成的△ABO是何种特殊三角形？并说明理由．                   

在弹性限度内，弹簧长度y（cm）是所挂物体的质量x（g）的一次函数．已知一根弹簧挂10g物体时的长度为11cm，挂30g物体时的长度为15cm．
（1）求y与x的函数表达式；
（2）当所挂物体的质量为14g时，求弹簧的长度．

如图，把长方形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．

（1）△BEF是等腰三角形吗？试说明理由；
（2）若AB＝8，DE＝10，求CF的长度．

作图题（不写作法，保留作图痕迹）：
（1）如图，已知△ABC，∠C=Rt∠，AC<BC，D为BC上一点，且到A、B两点的距离相等．用直尺和圆规，作出点D的位置；

（2）用直尺和圆规在如图所示的数轴上作出表示的点．

求下列各式中的x：
（1）已知，求x；        
（2）计算：；

观察下列等式：
=1-，=，=……，
将以上二个等式两边分别相加得：
++=1-++==
用你发现的规律解答下列问题：
（1）猜想并写出：=_______
（2）直接写出下列各式的计算结果：
①+++…+=_______
②+++…+=_______
（3）探究并计算：
+…+

同学们都知道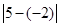，表示5与－2之差的绝对值，实际上也可理解为5与－2两数在数轴上所对应的两点之间的距离，试探索：
（1）＝_______．
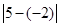（2）同理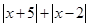表示数轴上有理数x所对应的点到－5和2所对应的两点距离之和，请你找出所有符合条件的整数x，使得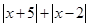＝7，这样的整数是_______．
（3）由以上探索猜想对于任何有理数x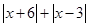，是否有最小值？如果有，写出最小值；如果没有，说明理由．

少儿图书馆上周借书记录（超过100册的部分记为正，少于100册的部分记为负）如下表：

星期一	星期二	星期三	星期四	星期五	星期六
+18	－6	+15	－12	0	+27

 
（1）上星期五借出多少册书？
（2）上个星期借书最多的一天比借书最少的一天多多少？
（3）上星期平均每天借出多少册书？

已知多项式（2x²＋ax－y＋6）－（2bx²－3x＋5y－1）．
（1）若多项式的值与字母x的取值无关，求a，b的值；
（2）在（1）的条件下，先化简多项式3（a²－ab＋b²）－（3a²＋ab＋b²），再求它的值；