初中数学解答题

如图， $\angle \mathit{AOB}=60°$，点 $P$为射线 $\mathit{OA}$上的一动点．过点 $P$作 $\mathit{PC}\perp \mathit{OB}$于点 $C$．点 $D$在 $\angle \mathit{AOB}$内，且满足 $\angle \mathit{APD}=\angle \mathit{OPC}$， $\mathit{DP}+\mathit{PC}=10$．

（1）当 $\mathit{PC}=6$时，求点 $D$到 $\mathit{OB}$的距离；

（2）在射线 $\mathit{OA}$上是否存在一定点 $M$，使得 $\mathit{MD}=\mathit{MC}$？若存在，请用直尺（不带刻度）和圆规作出点 $M$（不必写作法，但要保留作图痕迹），并求 $\mathit{OM}$的长；若不存在，说明理由．

$A$商场从某厂以75元 $/$件的价格采购一种商品，售价是100元 $/$件．厂家与商场约定：若商场一次性采购达到或超过400件，厂家按每件5元返利给 $A$商场．商场没有售完的，可以以65元 $/$件退还给厂家．设 $A$商场售出该商品 $x$件，问： $A$商场对这种商品的销量至少要多少时，他们的获利能达到9600元？

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle C=90°$， $\mathit{AD}$是 $\mathit{\Delta ABC}$的角平分线，点 $O$在边 $\mathit{AB}$上．过点 $A$、 $D$的圆的圆心 $O$在边 $\mathit{AB}$上，它与边 $\mathit{AB}$交于另一点 $E$．

（1）试判断 $\mathit{BC}$与圆 $O$的位置关系，并说明理由；

（2）若 $\mathit{AC}=6$， $\sin B=\frac{3}{5}$，求 $\mathit{AD}$的长．

某校4月份八年级的生物实验考查，有 $A$、 $B$、 $C$、 $D$四个考查实验，规定每位学生只参加其中一个实验的考查，并由学生自己抽签决定具体的考查实验．小明、小丽都参加了本次考查．

（1）小丽参加实验 $A$考查的概率是　　；

（2）用列表或画树状图的方法求小明、小丽都参加实验 $A$考查的概率．

某市教育局组织全市中小学教师开展“请千家”活动．活动过程中，教有局随机抽取了近两周家访的教师人数及家访次数，将采集到的全部数据按家访次数分成五类，由甲、乙两人分别绘制了下面的两幅统计图（图都不完整）．

请根据以上信息，解答下列问题：

（1）请把这幅条形统计图补充完整（画图后请标注相应的数据）；

（2）在采集到的数据中，近两周平均每位教师家访　　次；

（3）若该市有12000名教师，则近两周家访不少于3次的教师约有　　人．

如图，已知五边形 $\mathit{ABCDE}$是正五边形，连接 $\mathit{AC}$、 $\mathit{AD}$．证明： $\angle \mathit{ACD}=\angle \mathit{ADC}$．

对给定的一张矩形纸片 $\mathit{ABCD}$进行如下操作：先沿 $\mathit{CE}$折叠，使点 $B$落在 $\mathit{CD}$边上（如图① $)$，再沿 $\mathit{CH}$折叠，这时发现点 $E$恰好与点 $D$重合（如图② $)$

（1）根据以上操作和发现，求 $\frac{\mathit{CD}}{\mathit{AD}}$的值；

（2）将该矩形纸片展开．

①如图③，折叠该矩形纸片，使点 $C$与点 $H$重合，折痕与 $\mathit{AB}$相交于点 $P$，再将该矩形纸片展开．求证： $\angle \mathit{HPC}=90°$；

②不借助工具，利用图④探索一种新的折叠方法，找出与图③中位置相同的 $P$点，要求只有一条折痕，且点 $P$在折痕上，请简要说明折叠方法．（不需说明理由）

平面直角坐标系 $\mathit{xOy}$中，二次函数 $y=x^2-2\mathit{mx}+m^2+2m+2$的图象与 $x$轴有两个交点．

（1）当 $m=-2$时，求二次函数的图象与 $x$轴交点的坐标；

（2）过点 $P(0,m-1)$作直线 $l\perp y$轴，二次函数图象的顶点 $A$在直线 $l$与 $x$轴之间（不包含点 $A$在直线 $l$上），求 $m$的范围；

（3）在（2）的条件下，设二次函数图象的对称轴与直线 $l$相交于点 $B$，求 $\mathit{\Delta ABO}$的面积最大时 $m$的值．

日照间距系数反映了房屋日照情况．如图①，当前后房屋都朝向正南时，日照间距系数 $=L:(H-H_1)$，其中 $L$为楼间水平距离， $H$为南侧楼房高度， $H_1$为北侧楼房底层窗台至地面高度．

如图②，山坡 $\mathit{EF}$朝北， $\mathit{EF}$长为 $15m$，坡度为 $i=1:0.75$，山坡顶部平地 $\mathit{EM}$上有一高为 $22.5m$的楼房 $\mathit{AB}$，底部 $A$到 $E$点的距离为 $4m$．

（1）求山坡 $\mathit{EF}$的水平宽度 $\mathit{FH}$；

（2）欲在 $\mathit{AB}$楼正北侧山脚的平地 $\mathit{FN}$上建一楼房 $\mathit{CD}$，已知该楼底层窗台 $P$处至地面 $C$处的高度为 $0.9m$，要使该楼的日照间距系数不低于1.25，底部 $C$距 $F$处至少多远？

如图， $\mathit{AB}$为 $\odot O$的直径， $C$为 $\odot O$上一点， $\angle \mathit{ABC}$的平分线交 $\odot O$于点 $D$， $\mathit{DE}\perp \mathit{BC}$于点 $E$．

（1）试判断 $\mathit{DE}$与 $\odot O$的位置关系，并说明理由；

（2）过点 $D$作 $\mathit{DF}\perp \mathit{AB}$于点 $F$，若 $\mathit{BE}=3\sqrt{3}$， $\mathit{DF}=3$，求图中阴影部分的面积．

为了改善生态环境，某乡村计划植树4000棵．由于志愿者的支援，实际工作效率提高了 $20\%$，结果比原计划提前3天完成，并且多植树80棵，原计划植树多少天？

如图， $\angle A=\angle D=90°$， $\mathit{AC}=\mathit{DB}$， $\mathit{AC}$、 $\mathit{DB}$相交于点 $O$．求证： $\mathit{OB}=\mathit{OC}$．

泰州具有丰富的旅游资源，小明利用周日来泰州游玩，上午从 $A$、 $B$两个景点中任意选择一个游玩，下午从 $C$、 $D$、 $E$三个景点中任意选择一个游玩．用列表或画树状图的方法列出所有等可能的结果，并求小明恰好选中景点 $B$和 $C$的概率．

某软件科技公司20人负责研发与维护游戏、网购、视频和送餐共4款软件．投入市场后，游戏软件的利润占这4款软件总利润的 $40\%$．如图是这4款软件研发与维护人数的扇形统计图和利润的条形统计图．

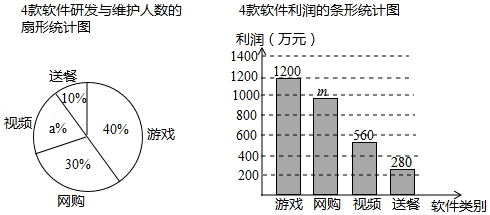
根据以上信息，回答下列问题

（1）直接写出图中 $a$， $m$的值；

（2）分别求网购与视频软件的人均利润；

（3）在总人数和各款软件人均利润都保持不变的情况下，能否只调整网购与视频软件的研发与维护人数，使总利润增加60万元？如果能，写出调整方案；如果不能，请说明理由．

如图，在平面直角坐标系中，二次函数 $y=(x-a)(x-3)(0<a<3)$的图象与 $x$轴交于点 $A$、 $B$（点 $A$在点 $B$的左侧），与 $y$轴交于点 $D$，过其顶点 $C$作直线 $\mathit{CP}\perp x$轴，垂足为点 $P$，连接 $\mathit{AD}$、 $\mathit{BC}$．

（1）求点 $A$、 $B$、 $D$的坐标；

（2）若 $\mathit{\Delta AOD}$与 $\mathit{\Delta BPC}$相似，求 $a$的值；

（3）点 $D$、 $O$、 $C$、 $B$能否在同一个圆上？若能，求出 $a$的值；若不能，请说明理由．