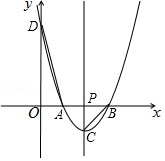
如图，在平面直角坐标系中，二次函数 的图象与 轴交于点 、 （点 在点 的左侧），与 轴交于点 ，过其顶点 作直线 轴，垂足为点 ，连接 、 ．
（1）求点 、 、 的坐标；
（2）若 与 相似，求 的值；
（3）点 、 、 、 能否在同一个圆上？若能，求出 的值；若不能，请说明理由．
+2.75+(－5
)
)+(－3
)+6
+(－2
)；
+(－
)+
+(－
)；相关知识点
推荐套卷
如图，在平面直角坐标系中，二次函数 的图象与 轴交于点 、 （点 在点 的左侧），与 轴交于点 ，过其顶点 作直线 轴，垂足为点 ，连接 、 ．
（1）求点 、 、 的坐标；
（2）若 与 相似，求 的值；
（3）点 、 、 、 能否在同一个圆上？若能，求出 的值；若不能，请说明理由．
粤公网安备 44130202000953号