初中数学计算题

（1）计算： $\sqrt{12}-\sqrt[3]{8}+|\sqrt{3}-2|$；

（2）化简： $(a+3)(a-2)-a(a-1)$．

问题：如图①，在 $\text{Rt}\Delta \text{ABC}$中， $\mathit{AB}=\mathit{AC}$， $D$为 $\mathit{BC}$边上一点（不与点 $B$， $C$重合），将线段 $\mathit{AD}$绕点 $A$逆时针旋转 $90°$得到 $\mathit{AE}$，连接 $\mathit{EC}$，则线段 $\mathit{BC}$， $\mathit{DC}$， $\mathit{EC}$之间满足的等量关系式为　              　；

探索：如图②，在 $\text{Rt}\Delta \text{ABC}$与 $\text{Rt}\Delta \text{ADE}$中， $\mathit{AB}=\mathit{AC}$， $\mathit{AD}=\mathit{AE}$，将 $\mathit{\Delta ADE}$绕点 $A$旋转，使点 $D$落在 $\mathit{BC}$边上，试探索线段 $\mathit{AD}$， $\mathit{BD}$， $\mathit{CD}$之间满足的等量关系，并证明你的结论；

应用：如图③，在四边形 $\mathit{ABCD}$中， $\angle \mathit{ABC}=\angle \mathit{ACB}=\angle \mathit{ADC}=45°$．若 $\mathit{BD}=9$， $\mathit{CD}=3$，求 $\mathit{AD}$的长．

绿色生态农场生产并销售某种有机产品，假设生产出的产品能全部售出．如图，线段 $\mathit{EF}$、折线 $\mathit{ABCD}$分别表示该有机产品每千克的销售价 $y_1$（元）、生产成本 $y_2$（元）与产量 $x\left(\mathit{kg}\right)$之间的函数关系．

（1）求该产品销售价 $y_1$（元）与产量 $x\left(\mathit{kg}\right)$之间的函数关系式；

（2）直接写出生产成本 $y_2$（元）与产量 $x\left(\mathit{kg}\right)$之间的函数关系式；

（3）当产量为多少时，这种产品获得的利润最大？最大利润为多少？

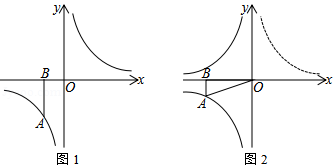
如图，在平面直角坐标系中，直线 $y=-\frac{1}{2}x$与反比例函数 $y=\frac{k}{x}(k\ne 0)$在第二象限内的图象相交于点 $A(m,1)$．

（1）求反比例函数的解析式；

（2）将直线 $y=-\frac{1}{2}x$向上平移后与反比例函数图象在第二象限内交于点 $B$，与 $y$轴交于点 $C$，且 $\mathit{\Delta ABO}$的面积为 $\frac{3}{2}$，求直线 $\mathit{BC}$的解析式．

已知关于 $x$的一元二次方程 $x^2+(2m+1)x+m^2-2=0$．

（1）若该方程有两个实数根，求 $m$的最小整数值；

（2）若方程的两个实数根为 $x_1$， $x_2$，且 ${(x_1-x_2)}^2+m^2=21$，求 $m$的值．

在2018年“新技术支持未来教育”的教师培训活动中，会议就“面向未来的学校教育、家庭教育及实践应用演示”等问题进行了互动交流，记者随机采访了部分参会教师，对他们发言的次数进行了统计，并绘制了不完整的统计表和条形统计图．

组别	发言次数 $n$	百分比
$A$	$0⩽n<3$	$10\%$
$B$	$3⩽n<6$	$20\%$
$C$	$6⩽n<9$	$25\%$
$D$	$9⩽n<12$	$30\%$
$E$	$12⩽n<15$	$10\%$
$F$	$15⩽n<18$	$m\%$

请你根据所给的相关信息，解答下列问题：

（1）本次共随机采访了　      　名教师， $m=$　      　；

（2）补全条形统计图；

（3）已知受访的教师中， $E$组只有2名女教师， $F$组恰有1名男教师，现要从 $E$组、 $F$组中分别选派1名教师写总结报告，请用列表法或画树状图的方法，求所选派的两名教师恰好是1男1女的概率．

化简： $\frac{4a+4b}{5\mathit{ab}}·\frac{15a^{2}b}{a^2-b^2}$．

已知点 $A(a,m)$在双曲线 $y=\frac{8}{x}$上且 $m<0$，过点 $A$作 $x$轴的垂线，垂足为 $B$．

（1）如图1，当 $a=-2$时， $P(t,0)$是 $x$轴上的动点，将点 $B$绕点 $P$顺时针旋转 $90°$至点 $C$．

①若 $t=1$，直接写出点 $C$的坐标；

②若双曲线 $y=\frac{8}{x}$经过点 $C$，求 $t$的值．

（2）如图2，将图1中的双曲线 $y=\frac{8}{x}(x>0)$沿 $y$轴折叠得到双曲线 $y=-\frac{8}{x}(x<0)$，将线段 $\mathit{OA}$绕点 $O$旋转，点 $A$刚好落在双曲线 $y=-\frac{8}{x}(x<0)$上的点 $D(d,n)$处，求 $m$和 $n$的数量关系．

用1块 $A$型钢板可制成2块 $C$型钢板和1块 $D$型钢板；用1块 $B$型钢板可制成1块 $C$型钢板和3块 $D$型钢板．现准备购买 $A$、 $B$型钢板共100块，并全部加工成 $C$、 $D$型钢板．要求 $C$型钢板不少于120块， $D$型钢板不少于250块，设购买 $A$型钢板 $x$块 $(x$为整数）．

（1）求 $A$、 $B$型钢板的购买方案共有多少种？

（2）出售 $C$型钢板每块利润为100元， $D$型钢板每块利润为120元．若将 $C$、 $D$型钢板全部出售，请你设计获利最大的购买方案．

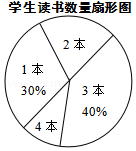
某校七年级共有500名学生，在“世界读书日”前夕，开展了“阅读助我成长”的读书活动．为了解该年级学生在此次活动中课外阅读情况，随机抽取 $m$名学生，调查他们课外阅读书籍的数量，将收集的数据整理成如下统计表和扇形图．

学生读书数量统计表

阅读量 $/$本	学生人数
1	15
2	$a$
3	$b$
4	5

（1）直接写出 $m$、 $a$、 $b$的值；

（2）估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本？

解方程组： $\left\{\begin{array}{c}x+y=10\\ 2x+y=16\end{array}\right.$

我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式（整数可看作分母为1的分数），那么无限循环小数如何表示为分数形式呢？请看以下示例：

例：将 $0.\dot{7}$化为分数形式

由于 $0.\dot{7}=0.777\dots$，设 $x=0.777\dots$①

则 $10x=7.777\dots$②

② $-$①得 $9x=7$，解得 $x=\frac{7}{9}$，于是得 $0.\dot{7}=\frac{7}{9}$．

同理可得 $0.\dot{3}=\frac{3}{9}=\frac{1}{3}$， $1.\dot{4}=1+0.\dot{4}=1+\frac{4}{9}=\frac{13}{9}$

根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）

（基础训练）

（1） $0.\dot{5}=$　    　， $5.\dot{8}=$　     　；

（2）将 $0.\dot{2}\dot{3}$化为分数形式，写出推导过程；

（能力提升）

（3） $0.\dot{3}1\dot{5}=$　    　， $2.0\dot{1}\dot{8}=$　    　；

（注 $:0.\dot{3}1\dot{5}=0.315315\dots$， $2.0\dot{1}\dot{8}=2.01818\dots )$

（探索发现）

（4）①试比较 $0.\dot{9}$与1的大小： $0.\dot{9}$　    　1（填“ $>$”、“ $<$”或“ $=$” $)$

②若已知 $0.\dot{2}8571\dot{4}=\frac{2}{7}$，则 $3.\dot{7}1428\dot{5}=$　     　．

（注 $:0.\dot{2}8571\dot{4}=0.285714285714\dots )$

为迎接“世界华人炎帝故里寻根节”，某工厂接到一批纪念品生产订单，按要求在15天内完成，约定这批纪念品的出厂价为每件20元，设第 $x$天（ $1⩽x⩽15$，且 $x$为整数）每件产品的成本是 $p$元， $p$与 $x$之间符合一次函数关系，部分数据如表：

天数 $\left(x\right)$	1	3	6	10
每件成本 $p$（元）	7.5	8.5	10	12

任务完成后，统计发现工人李师傅第 $x$天生产的产品件数 $y$（件）与 $x$（天）满足如下关系： $y=\left\{\begin{array}{c}2x+20(1⩽x<10,且x\mathit{为整数})\\ 40\left(10⩽x⩽15,且x\mathit{为整数}\right)\end{array}\right.$

设李师傅第 $x$天创造的产品利润为 $W$元．

（1）直接写出 $p$与 $x$， $W$与 $x$之间的函数关系式，并注明自变量 $x$的取值范围：

（2）求李师傅第几天创造的利润最大？最大利润是多少元？

（3）任务完成后，统计发现平均每个工人每天创造的利润为299元．工厂制定如下奖励制度：如果一个工人某天创造的利润超过该平均值，则该工人当天可获得20元奖金．请计算李师傅共可获得多少元奖金？

随州市新水一桥（如图1）设计灵感来源于市花 $--$兰花，采用蝴蝶兰斜拉桥方案，设计长度为258米，宽32米，为双向六车道，2018年4月3日通车．斜拉桥又称斜张桥，主要由索塔、主梁、斜拉索组成．某座斜拉桥的部分截面图如图2所示，索塔 $\mathit{AB}$和斜拉索（图中只画出最短的斜拉索 $\mathit{DE}$和最长的斜拉索 $\mathit{AC}$）均在同一水平面内， $\mathit{BC}$在水平桥面上．已知 $\angle \mathit{ABC}=\angle \mathit{DEB}=45°$， $\angle \mathit{ACB}=30°$， $\mathit{BE}=6$米， $\mathit{AB}=5\mathit{BD}$．

（1）求最短的斜拉索 $\mathit{DE}$的长；

（2）求最长的斜拉索 $\mathit{AC}$的长．

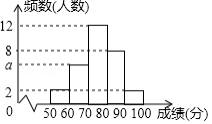
为了解某次“小学生书法比赛”的成绩情况，随机抽取了30名学生的成绩进行统计，并将统计情况绘成如图所示的频数分布直方图，已知成绩 $x$（单位：分）均满足“ $50⩽x<100$”．根据图中信息回答下列问题：

（1）图中 $a$的值为　      　；

（2）若要绘制该样本的扇形统计图，则成绩 $x$在“ $70⩽x<80$”所对应扇形的圆心角度数为　     　度；

（3）此次比赛共有300名学生参加，若将“ $x⩾80$”的成绩记为“优秀”，则获得“优秀“的学生大约有　      　人：

（4）在这些抽查的样本中，小明的成绩为92分，若从成绩在“ $50⩽x<60$”和“ $90⩽x<100$”的学生中任选2人，请用列表或画树状图的方法，求小明被选中的概率．