如图,在大楼 正前方有一斜坡 ,坡角 ,楼高 米,在斜坡下的点 处测得楼顶 的仰角为 ,在斜坡上的 处测得楼顶 的仰角为 ,其中点 , , 在同一直线上.
(1)求坡底 点到大楼距离 的值;
(2)求斜坡 的长度.

如图,反比例函数 过点 ,直线 与 轴交于点 ,过点 作 轴的垂线 交反比例函数图象于点 .
(1)求 的值与 点的坐标;
(2)在平面内有点 ,使得以 , , , 四点为顶点的四边形为平行四边形,试写出符合条件的所有 点的坐标.

在端午节来临之际,某商店订购了 型和 型两种粽子, 型粽子28元 千克, 型粽子24元 千克,若 型粽子的数量比 型粽子的2倍少20千克,购进两种粽子共用了2560元,求两种型号粽子各多少千克.
某学校为改善办学条件,计划采购 、 两种型号的空调,已知采购3台 型空调和2台 型空调,需费用39000元;4台 型空调比5台 型空调的费用多6000元.
(1)求 型空调和 型空调每台各需多少元;
(2)若学校计划采购 、 两种型号空调共30台,且 型空调的台数不少于 型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
如图,直线 交 轴于点 ,交 轴于点 ,与反比例函数 的图象有唯一的公共点 .
(1)求 的值及 点坐标;
(2)直线 与直线 关于 轴对称,且与 轴交于点 ,与双曲线 交于 、 两点,求 的面积.

如图所示,为测量旗台 与图书馆 之间的直线距离,小明在 处测得 在北偏东 方向上,然后向正东方向前进100米至 处,测得此时 在北偏西 方向上,求旗台与图书馆之间的距离.(结果精确到1米,参考数据 , )

新欣商场经营某种新型电子产品,购进时的价格为20元 件.根据市场预测,在一段时间内,销售价格为40元 件时,销售量为200件,销售单价每降低1元,就可多售出20件.
(1)写出销售量 (件)与销售单价 (元)之间的函数关系式;
(2)写出销售该产品所获利润 (元)与销售单价 (元)之间的函数关系式,并求出商场获得的最大利润;
(3)若商场想获得不低于4000元的利润,同时要完成不少于320件的该产品销售任务,该商场应该如何确定销售价格.
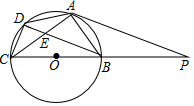
如图,四边形 内接于 , 为 的直径, 与 交于点 , 为 延长线上一点,连接 ,且 .
(1)求证: 为 的切线;
(2)若 , ,求 长;
(3)在(2)的条件下,若 ,求 的面积.
如图,我国一艘海监执法船在南海海域进行常态化巡航,在 处测得北偏东 方向距离为40海里的 处有一艘可疑船只正在向正东方向航行,我海监执法船便迅速沿北偏东 方向前往监视巡查,经过一段时间在 处成功拦截可疑船只.
(1)求 的度数;
(2)求我海监执法船前往监视巡查的过程中行驶的路程(即 长)?(结果精确到0.1海里, , ,

已知关于 的方程
(1)求证:无论 为何值,原方程都有实数根;
(2)若该方程的两实数根 、 为一菱形的两条对角线之长,且 ,求 值及该菱形的面积.
在大课间活动中,体育老师随机抽取了八年级甲、乙两个班部分女同学进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
|
分 组 |
频数 |
频率 |
|
第一组 |
3 |
0.15 |
|
第二组 |
|
0.3 |
|
第三组 |
7 |
0.35 |
|
第四组 |
4 |
|
(1)频数分布表中 , ,并将统计图补充完整;
(2)如果该校八年级共有女生180人,估计仰卧起坐一分钟完成30或30次以上的女学生有多少人;
(3)已知第一组中只有一个甲班同学,第四组中只有一个乙班同学,老师随机从这两个组中各选一名学生谈心得体会,用树状图或列表求所选两人正好都是甲班学生的概率.

某市总预算 亿元用三年时间建成一条轨道交通线.轨道交通线由线路敷设、搬迁安置、辅助配套三项工程组成.从2015年开始,市政府在每年年初分别对三项工程进行不同数额的投资.
2015年年初,对线路敷设、搬迁安置的投资分别是辅助配套投资的2倍、4倍.随后两年,线路敷设投资每年都增加 亿元,预计线路敷设三年总投资为54亿元时会顺利如期完工;搬迁安置投资从2016年年初开始逐年按同一百分数递减,依此规律,在2017年年初只需投资5亿元,即可顺利如期完工;辅助配套工程在2016年年初的投资在前一年基础上的增长率是线路敷设2016年投资增长率的1.5倍,2017年年初的投资比该项工程前两年投资的总和还多4亿元,若这样,辅助配套工程也可以如期完工.经测算,这三年的线路敷设、辅助配套工程的总投资资金之比达到 .
(1)这三年用于辅助配套的投资将达到多少亿元?
(2)市政府2015年年初对三项工程的总投资是多少亿元?
(3)求搬迁安置投资逐年递减的百分数.