古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

| A.36=15+21 | B.49=18+31 | C.25="9+16" | D.13=3+10 |
如图,在Rt△OAB中,∠AOB=90°,OA=4,OB=3.⊙O的半径为2,点P是线段AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x,PQ2=y,则y与x的函数图象大致是( ).
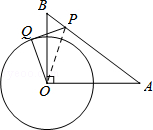
A.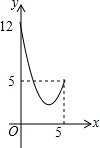 |
B.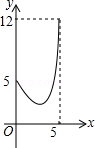 |
C.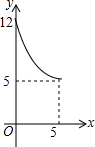 |
D.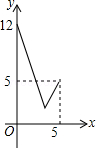 |
小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2﹣4ac>0;②c>1;③ab>0;④a﹣b+c<0.你认为其中正确的有( ).
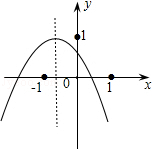
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,在矩形ABCD中,AB=4cm,AD=2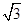 cm,E为CD边上的中点,点P从点A沿折线AE﹣EC运动到点C时停止,点Q从点A沿折线AB﹣BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P,Q同时开始运动,设运动时间为t(s),△APQ的面积为y(cm2),则y与t的函数关系的图象可能是( ).
cm,E为CD边上的中点,点P从点A沿折线AE﹣EC运动到点C时停止,点Q从点A沿折线AB﹣BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P,Q同时开始运动,设运动时间为t(s),△APQ的面积为y(cm2),则y与t的函数关系的图象可能是( ).
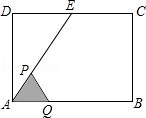
A.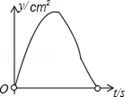 |
B.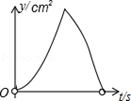 |
C.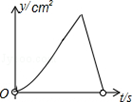 |
D.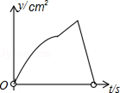 |
把抛物线y=2 -4x-5绕顶点旋转180º,得到的新抛物线的解析式是( )
-4x-5绕顶点旋转180º,得到的新抛物线的解析式是( )
A.y= -2 -4x-5 -4x-5 |
B.y=-2 +4x+5 +4x+5 |
C.y=-2 +4x-9 +4x-9 |
D.以上都不对 |
如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A8的坐标是( )

| A.(﹣8,0) | B.(0,8) | C.(0,8 ) ) |
D.(0,16) |
如图,正方形ABCD中,点E,F分别在AD,DC上,且△BEF为等边三角形,下列结论:
①DE=DF;②∠AEB=75°;③BE= DE;④AE+FC=EF.
DE;④AE+FC=EF.
其中正确的结论个数有( )

| A.1个 | B.2个 | C.3个 | D.4个 |
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0:③b>0;④x<2时,kx+b<x+a中,正确的个数是( )
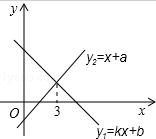
| A.1 | B.2 | C.3 | D.4 |
如图,ABCD是正方形场地,点E在DC的延长线上,AE与BC相交于点F.有甲、乙、丙三名同学同时从点A出发,甲沿着A﹣B﹣F﹣C的路径行走至C,乙沿着A﹣F﹣E﹣C﹣D的路径行走至D,丙沿着A﹣F﹣C﹣D的路径行走至D.若三名同学行走的速度都相同,则他们到达各自的目的地的先后顺序(由先至后)是( )

A.甲乙丙 B.甲丙乙 C.乙丙甲 D.丙甲乙
如图,在△ABC中,点E在AC上,点G在BC上,连接EG,AE=EG=5,过点E作ED⊥AB,垂足为D,过点G作GF⊥AC,垂足为F,此时恰有DE=GF=4.若BG=2 ,则sinB的值为( )
,则sinB的值为( )

A. |
B. |
C. |
D. |
对于任意实数a、b,定义f(a,b)=a2+5a-b,如:f(2,3)=22+5×2-3,若f(x,2)=4,则实数x的值是( )
| A.1或-6 | B.-1或6 | C.-5或1 | D.5或-1 |
如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )
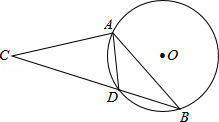
A.2﹣ B.
B. ﹣1 C.2 D.
﹣1 C.2 D.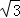 +1
+1
如图,已知⊙O的半径是R.C,D是直径AB同侧圆周上的两点,弧AC的度数为96°,弧BD的度数为36°,动点P在AB上,则PC+PD的最小值为( )
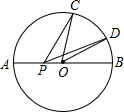
| A.2R | B.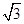 R R |
C.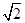 R R |
D.R |
如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD上一动点,则线段EP+FP的长最短为( )

| A.3 | B.4 | C.5 | D.6 |