河北省中考模拟一数学试卷
2014年11月1日河北省18座大型水库共蓄水22.06亿立方米,比10月1日多蓄水0.97亿立方米,则10月1日这18座大型水库共蓄水( )
| A.23.03亿立方米 | B.21.19亿立方米 |
| C.21.11亿立方米 | D.21.09亿立方米 |
如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
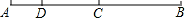
| A.4 | B.6 | C.8 | D.10 |
2014年6月18日中商网报道,一种重量为0.000106千克,机身由碳纤维制成,且只有昆虫大小的机器人是全球最小的无人机,0.000106用科学记数法可表示为( )
| A.1.06×10-4 | B.1.06×10-5 |
| C.10.6×10-5 | D.106×10-6 |
如图,在五边形ABCDE中,AB∥DE,若△ABE的面积为5,则△ABD的面积为( )
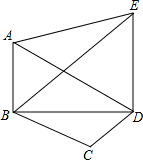
| A.4 | B.5 | C.10 | D.无法判断 |
已知单项式3xa+1y4与-2yb-2x3是同类项,则下列单项式,与它们属于同类项的是( )
| A.-5xb-3y4 | B.3xby4 | C.xay4 | D.-xayb+1 |
已知x=y≠- ,且xy≠0,下列各式:①x-3=y-3;②
,且xy≠0,下列各式:①x-3=y-3;② ;③
;③ ;④2x+2y=0,其中一定正确的有( )
;④2x+2y=0,其中一定正确的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
下列说法中不正确的是( )
| A.“某射击运动员射击一次,正中把靶心”属于随机事件 |
| B.“13名同学至少有两名同学的出生月份相同”属于必然事件 |
| C.“在标准大气压下,当温度降到-1℃时,水结成冰”属于随机事件 |
| D.“某袋中只有5个球,且都是黄球,任意摸出一球是白球”属于不可能事件 |
如图是石家庄某小区高层住户2014年的取暖费统计表,小宇家住1201(12楼)室,小鹏家住3301(33楼)室,小宇家和小鹏家的面积是一样的,该小区对28楼以上的住户的取暖费有优惠政策,在实施该政策以后,小宇发现小鹏家平均每平方米的取暖费比他家的少4.4元,则小宇家每平方米的取暖费为( )

| A.21元 | B.22元 | C.23元 | D.24元 |
如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )

| A.6 | B.8 | C.10 | D.无法确定 |
如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的中垂线上,则∠ADC的度数为( )
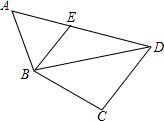
| A.75° | B.65° | C.63° | D.61° |
如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕点B逆时针旋转一定角度,点C′恰落在边BC上的高所在的直线上,则边BC在旋转过程中所扫过的面积为( )

| A.π | B.2π | C.3π | D.4π |
现已知线段a,b(a<b),∠MON=90°,求作Rt△ABO,使得∠O=90°,AB=b,小惠和小雷的作法分别如下.
小惠:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点A为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
小雷:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点O为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
则下列说法中正确的是( )
| A.小惠的作法正确,小雷的作法错误 |
| B.小雷的作法正确,小惠的作法错误 |
| C.两人的作法都正确 |
| D.两人的作法都错误 |
如图,在△ABC中,点E在AC上,点G在BC上,连接EG,AE=EG=5,过点E作ED⊥AB,垂足为D,过点G作GF⊥AC,垂足为F,此时恰有DE=GF=4.若BG=2 ,则sinB的值为( )
,则sinB的值为( )

A. |
B. |
C. |
D. |
芳芳用水管以均匀的速度向一个容器中注水,在注水过程中,水面的高度h与注水时间t之间的函数图象如图所示,最后芳芳将容器注满水,则这个容器的形状大致为( )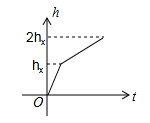
如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=- (x<0)交于C,D两点,点C的横坐标为-1,过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.下列说法:①b=6;②BC=AD;③五边形CDFOE的面积为35;④当x<-2时,y1>y2,其中正确的有( )
(x<0)交于C,D两点,点C的横坐标为-1,过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.下列说法:①b=6;②BC=AD;③五边形CDFOE的面积为35;④当x<-2时,y1>y2,其中正确的有( )

| A.1个 | B.2个 | C.3个 | D.4个 |
如图,在四边形ABCD中,AB=6,∠ABC=90°,E在CD上,连接AE,BE,∠DAE=75°,若四边形ABED是菱形,则EC的长度为 .

如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为 cm2.

罗非鱼又名非洲鲫鱼,是一种中小型鱼,每年的10月份是罗非鱼的捕捞期,某渔民有两个罗非鱼养殖鱼塘,在捕捞前期,为了估计鱼塘中罗非鱼的质量,该渔民从第一个鱼塘中随机捕捞若干条罗非鱼称得它们的质量(单位;kg),并将所得的数据绘制成了如图1图2所示的统计图(不完整)
(1)求该渔民所捞的罗非鱼的质量平均数、中位数和众数.
(2)当此渔民将罗非鱼的质量数据绘制成如图2所示的扇形统计图时,因某些原因没有标完数据,他只记得A扇形的圆心为36°,B扇形的中心角为84°,求A,B两个扇形分别表示的是哪种质量的罗非鱼;
(3)在同一时期,该渔民在第二个鱼塘捕捞了和第一个鱼塘相同条数的罗非鱼,并且求出罗非鱼质量的平均数也和第一个鱼塘的相同,但该鱼塘所捕捞的罗非鱼的质量的方差比第一个鱼塘的方差小,试判断哪个鱼塘的罗非鱼的质量的波动性较小.
如图,BE是⊙O的直径,点A,C,D,F都在⊙O上, ,连接CE,M是CE的中点,延长DE到点G,使得EG=DE,并且交AF的延长线于点G,此时F恰为AG的中点.
,连接CE,M是CE的中点,延长DE到点G,使得EG=DE,并且交AF的延长线于点G,此时F恰为AG的中点.
(1)若∠CDE=120°,CE=4 ,求⊙O的周长.
,求⊙O的周长.
(2)求证:2FE=CE.
(3)试探索:在 上是否存在一点N,使得四边形NMEF是轴对称图形,并说明理由.
上是否存在一点N,使得四边形NMEF是轴对称图形,并说明理由.
在某节习题课上,老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.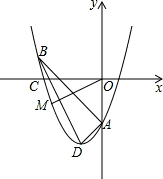
(1)某两位同学经过思考,对上述的二次函数进行了如下总结:
①该二次函数的图象经过点(1,3);
②当k<0时,该二次函数的图象与y轴的正半轴有交点;
请你判断上面两条结论是真命题还是假命题,并说明理由;
(2)若二次函数y=kx2+(k+1)x+2-4k的图象如图所示,该函数图象经过点B(-3,1)且与y轴交于点A,与x轴的负半轴交于点C,D为图象的顶点.
①求∠BAD的度数;
②点M在第三象限,且点M在二次函数图象上,连接OM.若∠ABD=∠MOC,求点M的横坐标.
在△ABC中,点D在直线AB上,在直线BC上取一点E,连接AE,DE,使得 AE=DE,DE交AC于点G,过点D作DF∥AC,交直线BC于点F,∠EAC=∠DEF.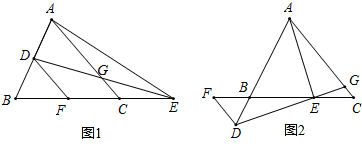
(1)当点E在BC的延长线上,D为AB的中点时,如图1所示.
①求证:∠EGC=∠AEC;
②若DF=3,求BE的长度;
(2)当点E在BC上,点D在AB的延长线上时,如图2所示,若CE=10,5EG=2DE,求AG的长度.
某自行车队根据队员速度的不同,分为快1组、快2组、慢1组和慢2组四个小组,在该车队的一次训练中,快1组和慢1组从甲地行进到乙地,剩下的组从乙地行进到甲地.快1组和慢1组同时从甲地出发,快1组的队员以高于慢1组队员10km/h的速度前行,快1组行驶一段时间后因某些原因又往回行驶(在往返过程中速度不变),最终与慢1组汇合,汇合后两组继续以各自的速度向乙地行进.设快1组和慢1组行驶的时间为t,与甲地的距离为s,s与t之间的函数图象如图所示.
(1)求OA解析式;
(2)已知甲地到乙地的距离为90km,在快1组与慢1组汇合时,慢2组(慢2组的速度与慢1组相同)由乙地开始出发,经过一段时间后,快1组和慢2组同时到达补给站.
①求此时慢2组与甲地之间的距离;
②若快2组在某一时刻也从乙地出发,速度与快1组相同,如果快2组不能比慢2组晚到甲地,求快2组比慢2组最多晚出发多少小时?
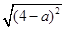 的结果为( )
的结果为( ) )÷
)÷ 的结果为 .
的结果为 . ,a3=
,a3= ,…an=
,…an= ,则a10的值为 .
,则a10的值为 . .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号