初中数学圆幂定理解答题

如图：AB是⊙O的直径，D、T是圆上两点，且AT平分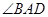，过点T作AD延长线的垂线PQ，垂足为C。

求证：PQ是⊙O的切线。
若⊙O的半径为4，TC=，求弦AD的长。

如图，在气象站台A的正西方向的B处有一台风中心，该台风中心以每小时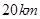的速度沿北偏东的BD方向移动，在距离台风中心内的地方都要受到其影响。

⑴台风中心在移动过程中，与气象台A的最短距离是多少？
⑵台风中心在移动过程中，气象台将受台风的影响，求台风影响气象台多长时间？

（本题8分）如图，AB为⊙O的直径，CD⊥AB于点E，交⊙O于点D，OF⊥AC于点F．

（1）请写出两条与BC有关的正确结论；
（2）当∠D=30°，BC=1时，求圆中阴影部分的面积．

如图，AD为⊙O的直径，作⊙O的内接等边三角形ABC.黄皓、李明两位同学的作法分别是：

黄皓：1. 作OD的垂直平分线，交⊙O于B，C两点，
2. 连结AB，AC，△ABC即为所求的三角形.
李明：1. 以D为圆心，OD长为半径作圆弧，交⊙O于B，C两点，
2. 连结AB，BC，CA，△ABC即为所求的三角形.
已知两位同学的作法均正确，请选择其中一种作法补全图形，并证明△ABC是等边三角形.

如图，在△ABC中，点O在AB上，以O为圆心的圆经过A，C两点，交AB于点D，已知2∠A +∠B =．

（1）求证：BC是⊙O的切线；
（2）若OA=6，BC=8，求BD的长．

已知：AB是⊙O的直径，D是⊙O上一动点，且D点与A点不重合，延长AD到C使CD＝AD，连结BC、BD.证明： AB＝BC.

如图①，AB为⊙O的直径，AD与⊙O相切于点A，DE与⊙O相切于点E，点C为DE延长线上一点，且CE=CB。

（1）求证：BC为⊙O的切线；
（2）如图②，连接AE，AE的延长线与BC的延长线交于点G。若，求线段BC和EG的长。

已知：如图8，△ABC中，AC＝BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于点E，交BC的延长线于点F．（12）

求证：（1）AD＝BD；　（2）DF是⊙O的切线．

(8分)如图，AB、CD为⊙O内两条相交的弦，交点为E，且AB=CD。则以下结论中：①AE=EC ②AD=BC  ③BE=EC  ④AD∥BC， 正确的有          。试证明你的结论。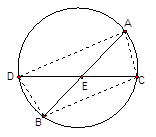

（本题10分）如图，AB为⊙O直径，BC切⊙O于B，CO交⊙O交于D，AD的延长线交BC于E，若∠C = 25°，求∠A的度数。

(7分)如图，在平面直角坐标中，以点M为圆心，以长为半经作圆M交轴于A，B两点，连结AM并延长交圆M于点P，连结PC交轴于点E。

（1）求点A，C的坐标
（2）求证：BE=2OE

如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC、AC于D、E两点，过点D作DF⊥AC，垂足为点F．

（1）求证：DF是⊙O的切线；
（2）若弧AE=弧DE，DF=2，求弧AD的长．

如图，△中，是它的角平分线，，在边上，以为直径的半圆经过点，交于点。

（1）求证：是的切线；
（2）若，连接，求证：∥；
（3）在（2）的条件下，若，求图中阴影部分的面积。

如图，在边长为1的等边△OAB中，以边AB为直径作⊙D，以D为圆心似长为半径作
圆O、C为半圆AB上不与A、B重合的一动点，射线AC交⊙O于点E，BC=a，AC=b，

（1）求证：AE=b+a；
（2）求a+b的最大值；
（3）若m是关于x的方程：x+ax=b+ab的一个根，求m的取值范围．

已知等边△ABC，边长为4，点D从点A出发，沿AB运动到点B，到点B停止运动．点E从A出发，沿AC的方向在直线AC上运动．点D的速度为每秒1个单位，点E的速度为每秒2个单位，它们同时出发，同时停止．以点E为圆心，DE长为半径作圆．设E点的运动时间为t秒．

(l)如图l，判断⊙E与AB的位置关系，并证明你的结论；
(2)如图2，当⊙E与BC切于点F时，求t的值；
(3)以点C为圆心，CE长为半径作⊙C，OC与射线AC交于点G．当⊙C与⊙E相切时，直接写出t的值为____